查看数据源：5a1cdbf1feda740007edb87d
已知椭圆 $G:\dfrac{x^2}3+y^2=1$，设过点 $P\left(0,\dfrac 32\right)$ 的直线 $l$ 与椭圆 $G$ 交于 $M,N$ 两点，点 $B$ 为椭圆 $G$ 的下顶点，且 $BM=BN$．则直线 $l$ 的方程为 \((\qquad)\)
A: $y=\pm x+\dfrac 32$
B: $y=\pm\dfrac{\sqrt 6}3x+\dfrac 32$
C: $y=\pm\dfrac{\sqrt 6}2x+\dfrac 32$
D: 以上答案对不对
【难度】
【出处】
无
【标注】
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的方程
    >
    椭圆的标准方程
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的性质
    >
    椭圆的垂径定理
  • 题型
    >
    解析几何
    >
    圆锥曲线中的参数取值及范围问题
【答案】
B
【解析】
如图，设弦 $MN$ 的中点 $E$ 的坐标为 $(m,n)$，连接 $OE$，$BE$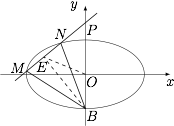．由椭圆的“垂径定理”与已知条件，有$$k_{BE}\cdot k_{PE}=-1,k_{OE}\cdot k_{PE}=-\dfrac 13,$$于是$$\dfrac{n+1}{m}\cdot\dfrac{n-\dfrac 32}{m-0}=-1,\dfrac{n}{m}\cdot\dfrac{n-\dfrac 32}{m}=-\dfrac 13,$$解得$$m=\pm\dfrac{\sqrt 6}2,n=\dfrac 12,$$于是直线 $l$ 的方程为 $y=\pm\dfrac{\sqrt 6}3x+\dfrac 32$．
题目 答案 解析 备注
0.141961s