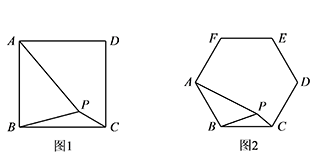
【难度】
【出处】
无
【标注】
-
如图1,在正方形 $ABCD$ 内有一点 $P$,$PA=\sqrt5$,$PB=\sqrt2$,$PC=1$,则 $\angle BPC$ 的度数为

-
如图2,若在正六边形 $ABCDEF$ 内有一点 $P$,且 $PA=2\sqrt{13}$,$PB=4$,$PC=2$,则 $\angle BPC$ 的度数为
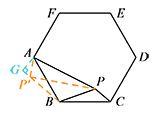
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2