设点 $A(1,0)$，$B(2,1)$，如果直线 $ax+by=1$ 与线段 $AB$ 有一个公共点，则 $a^2+b^2$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac{1}{5},+\infty\right)$
【解析】
记 $ax+by=1$ 为直线 $l$，则直线 $l$ 可以表示不经过原点的任意一条直线，同时 $l$ 与线段 $AB$ 有且只有一个公共点，直接考虑 $a^2+b^2$ 对于 $l$ 的几何意义．
因为原点到直线 $l$ 的距离为$$d=\dfrac{1}{\sqrt{a^2+b^2}},$$所以 $a^2+b^2=\dfrac {1}{d^2}$，本题转化为思考原点到满足条件的直线 $l$ 的距离 $d$ 的最值情况．显然 $d$ 没有最小值，即 $\sqrt{a^2+b^2}$ 没有最大值，下面考虑 $d$ 的最大值：
若 $P$ 是线段 $AB$ 与直线 $l$ 的公共点，则 $d\leqslant OP\leqslant OB$，当 $l\perp OP$ 时第一个等号成立，当 $P$ 与 $B$ 重合时第二个等号成立，如图：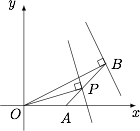
故 $d$ 的最大值为 $\sqrt 5$．故 $a^2+b^2$ 有最小值 $\dfrac{1}{5}$．
因为原点到直线 $l$ 的距离为$$d=\dfrac{1}{\sqrt{a^2+b^2}},$$所以 $a^2+b^2=\dfrac {1}{d^2}$，本题转化为思考原点到满足条件的直线 $l$ 的距离 $d$ 的最值情况．显然 $d$ 没有最小值，即 $\sqrt{a^2+b^2}$ 没有最大值，下面考虑 $d$ 的最大值：
若 $P$ 是线段 $AB$ 与直线 $l$ 的公共点，则 $d\leqslant OP\leqslant OB$，当 $l\perp OP$ 时第一个等号成立，当 $P$ 与 $B$ 重合时第二个等号成立，如图：
故 $d$ 的最大值为 $\sqrt 5$．故 $a^2+b^2$ 有最小值 $\dfrac{1}{5}$．
答案
解析
备注
