题目 已知函数 $f\left(x\right) ={x^3}- 3{x^2}+ ax + 2$，曲线 $y = f\left(x\right)$ 在点 $\left(0,2\right)$ 处的切线与 $x$ 轴交点的横坐标为 $- 2$． 问题1 求 $a$； 答案1 $a=1$ 解析1 $f(x)$ 的导函数$$f'(x)=3x^2-6x+a,$$于是曲线 $y=f(x)$ 在点 $(0,2)$ 处的切线方程为 $y=ax+2$．该直线与 $x$ 轴交于 $(-2,0)$，因此 $a=1$． 备注1 问题2 证明：当 $k < 1$ 时，曲线 $y = f\left(x\right)$ 与直线 $y = kx - 2$ 只有一个交点． 答案2 略 解析2 考虑方程 $f(x)=kx-2$，即$$x^3-3x^2+x+2=kx-2.$$由于 $x=0$ 不是该方程的解，因此只需要考虑 $x\neq 0$ 的情形，此时方程等价于$$k-1=\dfrac{x^3-3x^2+4}{x}.$$令 $g(x)=\dfrac{x^3-3x^2+4}{x}$，则 $g(x)$ 的导函数$$g'(x)=\dfrac{2x^3-3x^2-4}{x^2}=\dfrac{(x-2)(2x^2+x+2)}{x^2},$$因此当 $g(x)$ 在 $(-\infty ,0)$ 和 $(0,2)$ 上单调递减，在 $(2,+\infty )$ 上单调递增，在 $x=2$ 处取得极小值 $g(2)=0$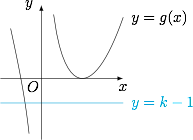．<img src="/static/images/3cf8845a15a78ecc39eaef8ed5b81391.png" class="img-responsive" />当 $x<0$ 时，$g(x)$ 单调递减，由于 $g(-1)=0$，而当 $-1<x<0$ 时$$g(x)=x^2-3x+\dfrac 4x<4+\dfrac 4x,$$因此 $g\left(\dfrac{4}{k-5}\right)<k-1$，于是当 $x<0$ 时，直线 $y=k-1$ 与函数 $g(x)$ 的图象有唯一公共点，且交点横坐标在区间 $\left(-1,\dfrac{4}{k-5}\right)$ 上．<br/>当 $x>0$ 时，$g(x)\geqslant 0$，此时直线 $y=k-1$ 与函数 $g(x)$ 的图象没有公共点．<br/>因此直线 $y=k-1$ 与函数 $g(x)$ 的图象有且只有一个公共点，原命题得证． 备注2