在 $\triangle ABC$ 中，$\angle ABC=40^\circ$，$\angle ACB=30^\circ$，$P$ 是 $\angle ABC$ 的平分线上一点，$\angle PCB=10^\circ$，求 $\angle PAB$ 的度数．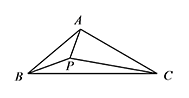
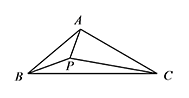
【难度】
【出处】
无
【标注】
【答案】
延长 $BA$ 到 $D$，使 $BD=BC$，连接 $DC,DP$．
所以 $\triangle BDP \cong \triangle BCP$，
所以 $\angle BDP=\angle BCP=10^\circ$，$PD=PC$，
所以 $\angle CPD=\angle DBC+\angle ADP+\angle PCB=60^\circ$，
所以 $\triangle CDP$ 是等边三角形．
所以 $\angle ACD=40^\circ,\angle ADC=70^\circ$，
则 $\angle CAD=70^\circ$，
所以 $AC=DC=PC$，$\angle CAP=80^\circ$，
所以 $\angle BAP=\angle BAC-\angle CAP=30^\circ$
所以 $\triangle BDP \cong \triangle BCP$，所以 $\angle BDP=\angle BCP=10^\circ$，$PD=PC$，
所以 $\angle CPD=\angle DBC+\angle ADP+\angle PCB=60^\circ$，
所以 $\triangle CDP$ 是等边三角形．
所以 $\angle ACD=40^\circ,\angle ADC=70^\circ$，
则 $\angle CAD=70^\circ$，
所以 $AC=DC=PC$，$\angle CAP=80^\circ$，
所以 $\angle BAP=\angle BAC-\angle CAP=30^\circ$
【解析】
略
答案
解析
备注
