已知 $\triangle ABC$ 中，$\angle BAC=2\angle ACB$，点 $D$ 是 $\triangle ABC$ 内一点，且 $AD=CD$，$BD=BA$，当 $\angle BAC\ne 90^\circ$ 时，求 $\angle DBC$ 与 $\angle ABC$ 度数的比值．
【难度】
【出处】
无
【标注】
【答案】
作 $\angle KCA=\angle BAC$，过 $B$ 点作 $BK\parallel AC$ 交 $CK$ 于点 $K$，连接 $DK$．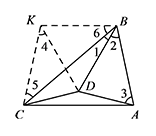
因为 $\angle BAC\ne 90^\circ$，所以四边形 $ABKC$ 是等腰梯形．
所以 $CK=AB$．
因为 $DC=DA$，
所以 $\angle DCA=\angle DAC$．
因为 $\angle KCA=\angle BAC$，
所以 $\angle KCD=\angle 3$，
所以 $\triangle KCD\cong \triangle BAD$，
所以 $\angle 2=\angle 4$，$KD=BD$，
所以 $KD=BD=BA=KC$．
因为 $BK\parallel AC$，
所以 $\angle ACB=\angle 6$．
因为 $\angle KCA=2\angle ACB$，
所以 $\angle 5=\angle ACB$，
所以 $\angle 5=\angle 6$，
所以 $KC=KB$，
所以 $KD=BD=KB$，
所以 $\angle KBD=60^\circ$．
因为 $\angle ACB=\angle 6=60^\circ-\angle 1$，
所以 $\angle BAC=2\angle ACB=2\angle 6=120^\circ-2\angle 1$．
因为 $\angle 1+\left(60^\circ-\angle 1\right)+\left(120^\circ-2\angle 1\right)+\angle 2=180^\circ$，
所以 $\angle 2=2\angle 1$，
所以 $\angle DBC$ 与 $\angle ABC$ 度数的比值为 $1:3$
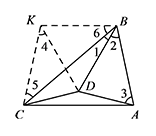因为 $\angle BAC\ne 90^\circ$，所以四边形 $ABKC$ 是等腰梯形．所以 $CK=AB$．
因为 $DC=DA$，
所以 $\angle DCA=\angle DAC$．
因为 $\angle KCA=\angle BAC$，
所以 $\angle KCD=\angle 3$，
所以 $\triangle KCD\cong \triangle BAD$，
所以 $\angle 2=\angle 4$，$KD=BD$，
所以 $KD=BD=BA=KC$．
因为 $BK\parallel AC$，
所以 $\angle ACB=\angle 6$．
因为 $\angle KCA=2\angle ACB$，
所以 $\angle 5=\angle ACB$，
所以 $\angle 5=\angle 6$，
所以 $KC=KB$，
所以 $KD=BD=KB$，
所以 $\angle KBD=60^\circ$．
因为 $\angle ACB=\angle 6=60^\circ-\angle 1$，
所以 $\angle BAC=2\angle ACB=2\angle 6=120^\circ-2\angle 1$．
因为 $\angle 1+\left(60^\circ-\angle 1\right)+\left(120^\circ-2\angle 1\right)+\angle 2=180^\circ$，
所以 $\angle 2=2\angle 1$，
所以 $\angle DBC$ 与 $\angle ABC$ 度数的比值为 $1:3$
【解析】
略
答案
解析
备注
