如图，$\triangle ABC$ 和 $\triangle BEC$ 均为等腰直角三角形，且 $\angle ACB=\angle BEC=90^{\circ}$，$AC=4\sqrt{2}$，点 $P$ 为线段 $BE$ 延长线上一点，连接 $CP$ 以 $CP$ 为直角边向下作等腰直角 $\triangle CPD$，线段 $BE$ 与 $CD$ 相交于点 $F$．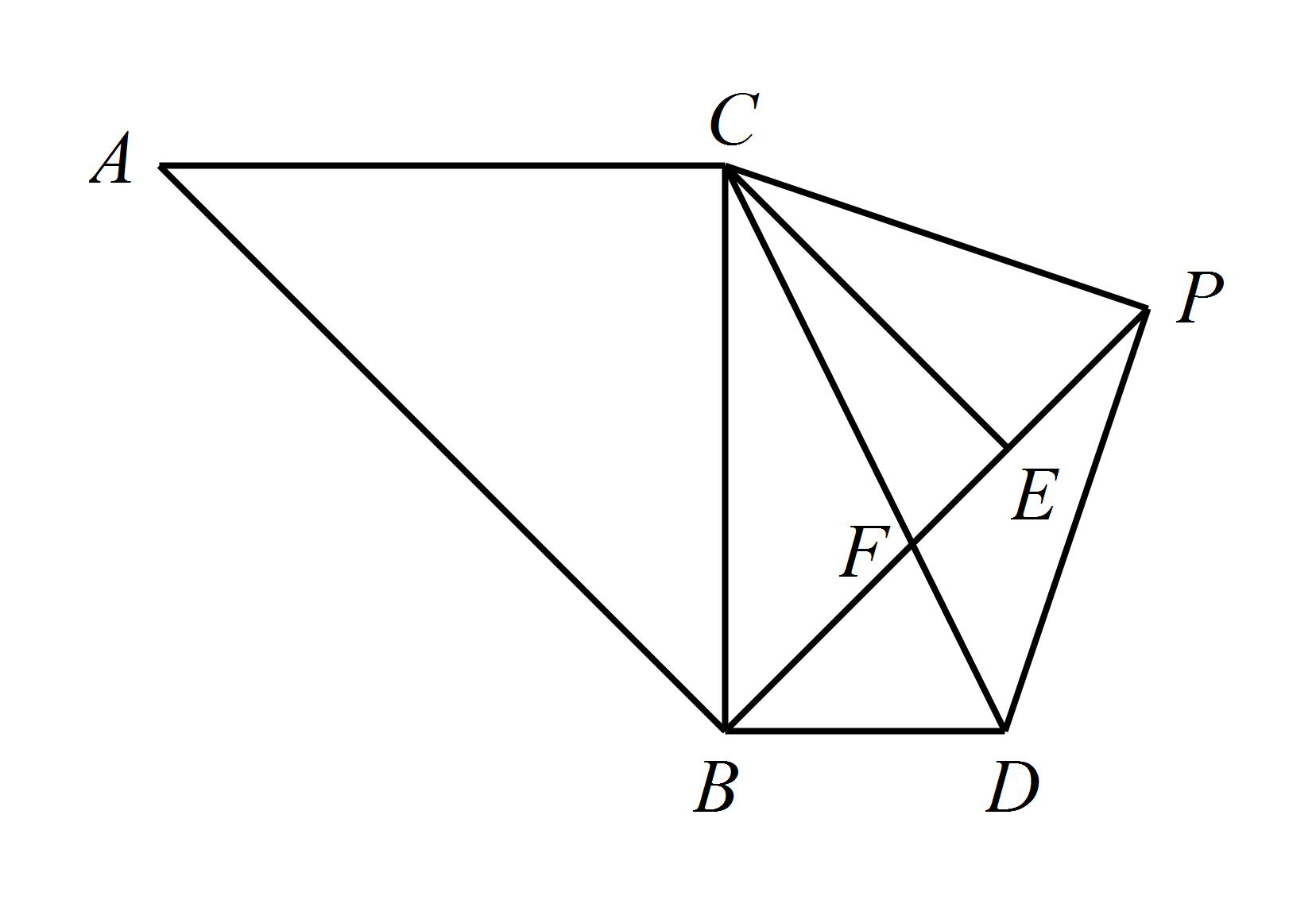
【难度】
【出处】
无
【标注】
-
求证：$\dfrac{PC}{CD }=\dfrac{CE}{ CB}$；标注答案因为 $\triangle BCE$ 和 $\triangle CDP$ 均为等腰直角三角形，
所以 $\angle ECB=\angle PCD=45^{\circ}$，$\angle CEB=\angle CPD=90^{\circ}$，
所以 $\triangle BCE\backsim\triangle DCP $，
所以 $\dfrac{PC}{CD }=\dfrac{CE}{ CB}$解析略 -
连接 $BD$，请你判断 $AC$ 与 $BD$ 有什么位置关系？并说明理由；标注答案$AC\parallel BD$．理由如下：
因为 $\angle PCE+\angle ECD=\angle BCD+\angle ECD=45^{\circ}$，
所以 $\angle PCE=\angle BCD $．
又因为 $\dfrac{PC}{CD }=\dfrac{CE}{ CB} $，
所以 $\triangle PCE\backsim\triangle DCB $．
所以 $\angle CBD=\angle CEP=90^{\circ}$．
因为 $\angle ACB=90^{\circ} $，
所以 $\angle ACB=\angle CBD$．
所以 $AC\parallel BD$解析略 -
设 $PE=x$，$\triangle PBD$ 的面积为 $S$，求 $S$ 与 $x$ 之间的函数关系式；标注答案作 $PM\perp BD$ 于点 $M$．
因为 $AC=4\sqrt{2}$，$\triangle ABC$ 和 $\triangle BEC$ 均为等腰直角三角形，
所以 $BE=CE=4$．
因为 $\triangle PCE\backsim\triangle DCB$，
所以 $\dfrac{CE}{CB }=\dfrac{PE}{BD } $，
即 $\dfrac{4}{4\sqrt{2} }=\dfrac{x}{ BD}$，
所以 $BD=\sqrt{2}x$．
因为 $\angle PBM=\angle CBD-\angle CBP=45^{\circ}$，$BP=BE+PE=4+x $，
所以 $PM=\dfrac{4+x}{\sqrt{2} }$，
所以 $\triangle PBD$ 的面积 $S=\dfrac12BD\cdot PM=\dfrac12\times \sqrt{2}x\times \dfrac{4+x}{\sqrt{2} }=\dfrac12x^2+2x$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
