已知:如图 ①,在平行四边形 $ABCD$ 中,$AB=3 \ {\mathrm {cm}}$,$BC=5 \ {\mathrm {cm}}$.$AC\perp AB$.$\triangle ACD$ 沿 $AC$ 的方向匀速平移得到 $\triangle PNM$,速度为 $1 \ {\mathrm {cm}}{/}{\mathrm s}$;同时,点 $Q$ 从点 $C$ 出发,沿 $CB$ 方向匀速运动,速度为 $1 \ {\mathrm {cm}}{/}{\mathrm s}$,当 $\triangle PNM$ 停止平移时,点 $Q$ 也停止运动.如图 ②,设运动时间为 $t\left({\mathrm s}\right)\left(0<t<4\right)$.
解答下列问题: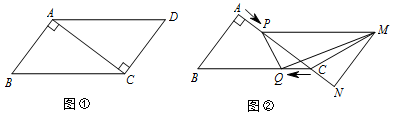
解答下列问题:

【难度】
【出处】
无
【标注】
-
是否存在某一时刻 $t$,使 $S_{\triangle QMC}:S_{四边形ABQP}=1:4$?若存在,求出 $t$ 的值;若不存在,请说明理由.标注答案因为 $PM\parallel BC$,
所以 ${S_{\triangle PQC}} = {S_{\triangle MQC}}$.
若 $S_{\triangle QMC}:S_{四边形 ABQP}=1:4$,则 $S_{\triangle QMC}:S_{\triangle ABC}=1:5$,
即:$ - \dfrac{3}{10}{t^2} + \dfrac{6}{5}t = \dfrac{1}{5} \times 6$,整理得:${t^2} - 4t + 4 = 0$,解得 $t = 2$.
答:当 $t=2$ 时,$S_{\triangle QMC}:S_{四边形 ABQP}=1:4$.解析略 -
是否存在某一时刻 $t$,使 $PQ\perp MQ$?若存在,求出 $t$ 的值;若不存在,请说明理由.标注答案若 $PQ \perp MQ$,则 $\angle MQP=\angle PDQ=90^\circ $.
因为 $MP\parallel BC$,
所以 $\angle MPQ=\angle PQD$,
所以 $\triangle MQP\backsim \triangle PDQ$,
所以 $\dfrac{PM}{PQ} = \dfrac{PQ}{DQ}$,
所以 $PQ^2 = PM \times DQ$,
即:$PD^2 + DQ^2 = PM \times DQ$,由 $CD = \dfrac{16 - 4t}{5}$,
所以 $DQ = CD-CQ = \dfrac{16 - 9t}{5}$,
故 ${\left(\dfrac{12 - 3t}{5}\right)^2} + {\left(\dfrac{16 - 9t}{5}\right)^2} = 5 \times \dfrac{16 - 9t}{5}$,整理得 $2{t^2} - 3t = 0$,
解得 $t_1=0$(舍),$t_2=\dfrac 32$.
答:当 $t = \dfrac{3}{2}$ 时,$PQ \perp MQ$.解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2