已知直线过点 $M(2,1)$ 且与 $x$、$y$ 轴正半轴分别交于 $A$、$B$ 两点，$O$ 为坐标原点．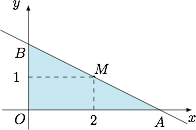
【难度】
【出处】
无
【标注】
-
求三角形 $AOB$ 面积的最小值；标注答案$ 4 $解析如图，设直线在第一象限内的线段被 $M$ 平分时与 $x$ 轴、$y$ 轴的交点分别为 $P$、$Q$．接下来证明此时三角形 $AOB$ 的面积最小．
若不然，假设 $AM<BM$，则\[\begin{split}S_{\triangle AOB}&=S_{\triangle POQ}-S_{\triangle MAP}+S_{\triangle MBQ}\\&=S_{\triangle POQ}-\dfrac{1}{2} MP\cdot \left(AM-BM\right)\cdot\sin\angle AMP\\&>S_{\triangle POQ},\end{split}\]当 $AM>BM$ 时类似．
因此当 $M$ 平分 $AB$ 时，三角形 $AOB$ 的面积最小，最小值为 $4$． -
求三角形 $AOB$ 周长的最小值．标注答案$ 10 $解析过 $M$ 作圆 $E$ 与 $x$ 轴、$y$ 轴均相切，作圆 $E$ 在 $M$ 处的切线，此时三角形 $AOB$ 的周长最小，为 $OP+OQ$，如图．
若不然，$AB$ 为圆 $E$ 的割线，此时可以作与该割线平行的切线，则显然有三角形 $AOB$ 的周长大于切线与两坐标轴围成的三角形的周长，而切线与坐标轴围成的三角形周长为 $OP+OQ$，故此时 $\triangle AOB$ 的周长大于 $OP+OQ$，如图．
经计算可得圆 $E:(x-5)^2+(y-5)^2=25$，$OP+OQ=10$，于是三角形 $AOB$ 周长的最小值为 $10$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
