已知椭圆 $C:x^2+2y^2=4$．
【难度】
【出处】
2014年高考北京卷（理）
【标注】
-
求椭圆 $C$ 的离心率；标注答案离心率 $e=\dfrac ca=\dfrac{\sqrt 2}2$解析根据题意，椭圆的长半轴长 $a=2$，短半轴长 $b=\sqrt 2$，因此半焦距 $c=\sqrt{a^2-b^2}=\sqrt 2$，离心率 $e=\dfrac ca=\dfrac{\sqrt 2}2$．
-
设 $O$ 为原点，若点 $A$ 在椭圆 $C$ 上，点 $B$ 在直线 $y=2$ 上，且 $OA\perp OB$，试判断直线 $AB$ 与圆 $x^2+y^2=2$ 的位置关系，并证明你的结论．标注答案直线 $AB$ 与圆 $x^2+y^2=2$ 相切解析设 $|OA|=r_1$，$|OB|=r_2$，点 $A$ 的坐标为 $A(r_1\cos\theta,r_1\sin\theta)$，其中 $\theta$ 表示以 $Ox$ 为始边，$OA$ 为终边的最小正角．
由 $OA\perp OB$ 可得点 $B$ 的坐标为 $B\left(r_2\cos\left(\theta\pm\dfrac{\pi}2\right),r_2\sin\left(\theta\pm\dfrac{\pi}2\right)\right)$．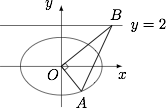
由点 $A$ 在椭圆上，点 $B$ 在直线 $y=2$ 上，可得$$r_1^2\cos^2\theta+2r_1^2\sin^2\theta=4,r_2\sin\left(\theta\pm\dfrac{\pi}2\right)=2,$$因此点 $O$ 到直线 $AB$ 的距离 $d$ 满足$$\dfrac{1}{d^2}=\dfrac{1}{r_1^2}+\dfrac{1}{r_2^2}=\dfrac{\cos^2\theta+2\sin^2\theta}4+\dfrac{\cos^2\theta}4=\dfrac 12,$$即 $d=\sqrt 2$．因此直线 $AB$ 与圆 $x^2+y^2=2$ 相切．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
