已知函数 $f(x)=\ln (1+x)$,$g(x)=kx$,$k\in \mathbb R$.
【难度】
【出处】
无
【标注】
-
证明:当 $x>0$ 时,$f(x)<x$;标注答案略解析根据题意,当 $x>0$ 时,有$$\left(f(x)-x\right)'=\dfrac 1{1+x}-1=\dfrac{-x}{1+x}<0,$$于是命题得证(如图).
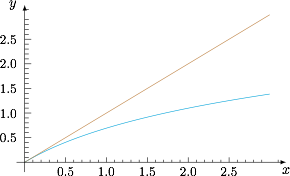
-
证明:当 $k<1$ 时,存在 $x_0>0$,使得对任意 $x\in (0,x_0)$,恒有 $f(x)>g(x)$;标注答案略解析考虑$$\left(f(x)-g(x)\right)'=\dfrac{1}{x+1}-k,$$于是当 $0<x<\dfrac 1k-1$ 时必然有$$\left(f(x)-g(x)\right)'>0,$$于是函数 $f(x)-g(x)$ 在 $\left(0,\dfrac 1k-1\right)$ 上单调递增,又 $f(0)-g(0)=0$,于是取 $x_0=\dfrac 1k-1$ 即可证明命题成立.
-
确定 $k$ 的所有可能取值,使得存在 $t>0$,对任意 $x\in (0,t)$,恒有 $\left|f(x)-g(x)\right|<x^2$.标注答案$k=1$解析根据题意当 $x\to 0+$ 时,有$$-x^2<f(x)-g(x)<x^2,$$即$$\begin{cases}\ln (1+x)-kx-x^2<0,\\\ln(1+x)-kx+x^2>0,\end{cases}$$记$$h_1(x)=\ln (1+x)-kx-x^2,\quad h_2(x)=\ln (1+x)-kx+x^2,$$此时注意到$$h_1(0)=h_2(0)=0,$$于是$$h_1'(0)\leqslant 0 \leqslant h_2'(0),$$即$$1-k\leqslant 0 \leqslant 1-k,$$因此 $k=1$.
事实上当 $k=1$ 时,在 $0<x<1$ 时,有\[\begin{split}h_1'(x)=&\dfrac{1}{1+x}-1-2x=\dfrac{-2x^2-3x}{1+x}<0,\\h_2'(x)=&\dfrac{1}{1+x}-1+2x=\dfrac{x+2x^2}{1+x}>0,\end{split}\]结合$$h_1(0)=h_2(0)=0,$$于是有$$h_1(x)<0<h_2(x)$$成立,即$$\left|f(x)-g(x)\right|<x^2$$成立,符合题意.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3