已知函数 $f\left(x\right)$ 满足：$f\left(x\right)\geqslant |x|$ 且 $f\left(x\right)\geqslant 2^x,x\in {\mathbb R}$． \((\qquad)\)
【难度】
【出处】
2016年高考浙江卷（文）
【标注】
【答案】
B
【解析】
本题考查抽象函数，利用所给的绝对值函数和指数函数比较单调性即可说明，也可以借助函数的图象来证明．由题知\[f\left(x\right)\geqslant \mathrm{max}\left\{|x|,2^x\right\}.\]取 $b=-2$，$f\left(0\right)\geqslant 2^0=1$，此时 $f\left(0\right)$ 与 $2$ 的大小不确定，若 $f\left(0\right)<2$，则A不成立；
由 $2^a\leqslant f\left(a\right)\leqslant 2^b$ 可得 $a\leqslant b$，所以B正确；
取 $b=2$，$f\left(-3\right)\geqslant |-3|=3>2$，所以C不成立；
取 $b=1$，$f\left(-2\right)\geqslant |-2|=2>1$，所以D不成立．
因此答案为B．
事实上，本题可以借助图象来分析：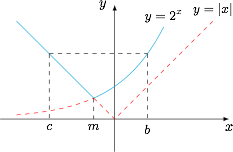
$f\left(x\right)$ 的图象在图中的实线上方（包括实线），以选项B的情况为例，设 $2^m=|m|$，则由题意可得 $b\geqslant m$，再设 $2^b=|c|\left(c<0\right)$，则 $a$ 的取值集合是 $\left[c,b\right]$ 的子集，如图所示．
由 $2^a\leqslant f\left(a\right)\leqslant 2^b$ 可得 $a\leqslant b$，所以B正确；
取 $b=2$，$f\left(-3\right)\geqslant |-3|=3>2$，所以C不成立；
取 $b=1$，$f\left(-2\right)\geqslant |-2|=2>1$，所以D不成立．
因此答案为B．
事实上，本题可以借助图象来分析：
$f\left(x\right)$ 的图象在图中的实线上方（包括实线），以选项B的情况为例，设 $2^m=|m|$，则由题意可得 $b\geqslant m$，再设 $2^b=|c|\left(c<0\right)$，则 $a$ 的取值集合是 $\left[c,b\right]$ 的子集，如图所示．
题目
答案
解析
备注
