查看数据源：59461725a26d28000bb86ea5
已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）所在平面内有一个不与原点重合的点 $P(x_0,y_0)$，过 $P$ 作 $E$ 的任意两条割线 $AB,CD$，其中 $A,B,C,D$ 均在椭圆 $E$ 上．证明：直线 $AC$ 和 $BD$ 的交点在定直线上．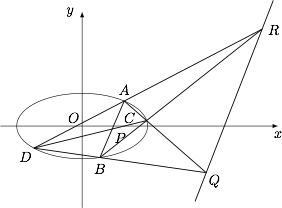
【难度】
【出处】
无
【标注】
  • 题型
    >
    解析几何
    >
    圆锥曲线的性质证明问题
  • 知识点
    >
    解析几何
    >
    直线与圆锥曲线
    >
    极点极线的调和性质
【答案】
略
【解析】
设 $AB$ 与 $CD$，$AC$ 与 $BD$ 的交点分别为 $P(x_0,y_0)$，$Q(x_1,y_1)$，只需要证明 $\dfrac{x_0x_1}{a^2}+\dfrac{y_0y_1}{b^2}=1$ 即可．设 $A\left(a\cos\alpha,b\sin\alpha\right)$，$B\left(a\cos\beta,b\sin\beta\right)$，$C\left(a\cos\gamma,b\sin\gamma\right)$，$D\left(a\cos\delta,b\sin\delta\right)$，则\[\begin{split} &AB:\dfrac xa\cdot \cos\dfrac{\alpha+\beta}2+\dfrac yb\cdot \sin\dfrac{\alpha+\beta}2=\cos\dfrac{\alpha-\beta}2,\\ &CD:\dfrac xa\cdot \cos\dfrac{\gamma+\delta}2+\dfrac yb\cdot \sin\dfrac{\gamma+\delta}2=\cos\dfrac{\gamma-\delta}2,\end{split}\]于是直线 $AB$ 与 $CD$ 的交点坐标为$$\left(a\cdot \dfrac{\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma+\delta}2-\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\cos\dfrac{\alpha+\beta}2\sin\dfrac{\gamma+\delta}2-\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma+\delta}2},b\cdot \dfrac{\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\sin\dfrac{\gamma+\delta}2}\right)$$即$$\left(a\cdot \dfrac{\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2-\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma +\delta}2}{\sin\dfrac{\alpha+\beta-\gamma-\delta}2},b\cdot\dfrac{\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\sin\dfrac{\alpha+\beta-\gamma-\delta}2}\right),$$交换 $\gamma$ 和 $\beta$ 就可以得到 $AC$ 与 $BD$ 的交点坐标，为$$\left(a\cdot \dfrac{\sin\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2-\cos\dfrac{\alpha-\gamma}2\sin\dfrac{\beta +\delta}2}{\sin\dfrac{\alpha+\gamma-\beta-\delta}2},b\cdot\dfrac{\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2}{\sin\dfrac{\alpha+\gamma-\beta-\delta}2}\right).$$于是我们只需证明\[\begin{split}& \left(\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2-\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma +\delta}2\right)\cdot\left(\sin\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2-\cos\dfrac{\alpha-\gamma}2\sin\dfrac{\beta +\delta}2\right) \\ &\qquad\qquad +\left(\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2\right)\cdot \left(\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2\right)\\ &\qquad\qquad\qquad\qquad\qquad \qquad\qquad \qquad\qquad \qquad\qquad \qquad\qquad =\sin\dfrac{\alpha+\beta-\gamma-\delta}2\cdot \sin\dfrac{\alpha+\gamma-\beta-\delta}2.\end{split}\]事实上，有\[\begin{split} LHS&=\cos\dfrac{\gamma-\delta}2\cos\dfrac{\beta-\delta}2\left(\sin\dfrac{\alpha+\beta}2\sin\dfrac{\alpha+\gamma}2+\cos\dfrac{\alpha+\beta}2\cos\dfrac{\alpha+\gamma}2\right)\\
&\qquad \qquad +\cos\dfrac{\gamma-\delta}2\cos\dfrac{\alpha-\gamma}2\left(-\sin\dfrac{\alpha+\beta}2\sin\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\beta+\delta}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\delta}2\left(-\sin\dfrac {\gamma+\delta}2\sin\dfrac{\alpha+\gamma}2-\cos\dfrac {\gamma+\delta}2\cos\dfrac{\alpha+\gamma}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\alpha-\gamma}2\left(\sin\dfrac{\gamma+\delta}2\sin\dfrac{\beta+\delta}2+\cos\dfrac{\gamma+\delta}2\cos\dfrac{\beta+\delta}2\right)\\
&=\cos\dfrac{\gamma-\delta}2\cos\dfrac{\beta-\delta}2\cos\dfrac{\beta-\gamma}2-\cos\dfrac{\gamma-\delta}2\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\alpha-\delta}2\\
&\qquad \qquad-\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\delta}2\cos\dfrac{\alpha-\delta}2+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta-\gamma}2\\
&=\cos\dfrac{\gamma-\delta }2\cos\left(\dfrac{\alpha-\beta}2+\dfrac{\delta-\alpha}2\right)\cos\dfrac{\beta-\gamma}2-\cos\dfrac{\gamma-\delta}2\cos\left(\dfrac{\alpha-\beta}2+\dfrac{\beta-\gamma}2\right)\cos\dfrac{\delta-\alpha}2\\
&\qquad \qquad-\cos\dfrac{\alpha-\beta}2\cos\left(\dfrac{\beta-\gamma}2+
\dfrac{\gamma-\delta}2\right)\cos\dfrac{\delta-\alpha}2+\cos\dfrac{\alpha-\beta}2\cos\left(\dfrac{\gamma-\delta}2+\dfrac{\delta-\alpha}2\right)\cos\dfrac{\beta-\gamma}2\\
&=\sin\dfrac{\alpha-\beta}2\sin\dfrac{\beta-\gamma}2\cos\dfrac{\gamma-\delta}2\cos\dfrac{\delta-\alpha}2-\sin\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\gamma}2\cos\dfrac{\gamma-\delta}2\sin\dfrac{\delta-\alpha}2\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\beta-\gamma}2\sin\dfrac{\gamma-\delta}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\gamma}2\sin\dfrac{\gamma-\delta}2\sin\dfrac{\delta-\alpha}2\\
&=\sin\dfrac{\alpha-\beta}2\cos\dfrac{\gamma-\delta}2\left(\sin\dfrac{\beta-\gamma}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\beta-\gamma}2\sin\dfrac{\delta -\alpha}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma-\delta}2\left(\sin\dfrac{\beta-\gamma}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\beta-\gamma}2\sin\dfrac{\delta-\alpha}2\right)\\
&=\sin\dfrac{\alpha-\beta}2\cos\dfrac{\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2\\
&=\sin\dfrac{\alpha-\beta+\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2\\
&=RHS,\end{split}\]因此原命题得证．
答案 解析 备注
0.163152s