设 $O$ 为坐标原点，$F_{1}$，$F_{2}$ 是双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} =1$（$a>0,b>0$）的焦点，若在双曲线上存在点 $P$，满足 $ \angle F_1P F_2=60^{\circ}$，$\left| {OP} \right| = \sqrt 7 a$，则该双曲线的渐近线方程为 \((\qquad)\)
【难度】
【出处】
2010年高考浙江卷（文）
【标注】
【答案】
D
【解析】
不妨设点 $P$ 在双曲线的右支上，设焦距为 $ 2c$，$\left| {P}{F_1} \right| =m$，$\left| {P}{F_2} \right| =n$．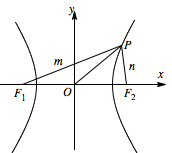
法一：根据双曲线定义有 $m-n=2a\cdots\cdots$ ①，
在 $\triangle PF_1F_2$ 中应用余弦定理有 $m^2+n^2-2mn\cos 60^{\circ}=4c^2\cdots\cdots$ ②，
又 $\overrightarrow {PF_1}+\overrightarrow {PF_2}=2\overrightarrow {PO}$，两边平方得 $m^2+n^2+2mn\cos 60^{\circ}=4\cdot 7a^2\cdots\cdots$ ③，
由 ①②③ 消去 $m,n$ 得到 $a,c$ 的关系 $3a^2=c^2$，然后结合 $a^2+b^2=c^2$ 易得 $b=\sqrt 2a$，所以选D．
法二：分别在 $ \triangle {{P}{F_1}{F_2}}$、$ \triangle {{P}{F_1}{O}}$、$ \triangle {{P}{F_2}{O}}$ 中应用余弦定理，再结合 $ m-n=2a$，消去 $ m$，$n$，得到 $3{a^2}={c^2}$，即得 $b=\sqrt 2a $．
法一：根据双曲线定义有 $m-n=2a\cdots\cdots$ ①，在 $\triangle PF_1F_2$ 中应用余弦定理有 $m^2+n^2-2mn\cos 60^{\circ}=4c^2\cdots\cdots$ ②，
又 $\overrightarrow {PF_1}+\overrightarrow {PF_2}=2\overrightarrow {PO}$，两边平方得 $m^2+n^2+2mn\cos 60^{\circ}=4\cdot 7a^2\cdots\cdots$ ③，
由 ①②③ 消去 $m,n$ 得到 $a,c$ 的关系 $3a^2=c^2$，然后结合 $a^2+b^2=c^2$ 易得 $b=\sqrt 2a$，所以选D．
法二：分别在 $ \triangle {{P}{F_1}{F_2}}$、$ \triangle {{P}{F_1}{O}}$、$ \triangle {{P}{F_2}{O}}$ 中应用余弦定理，再结合 $ m-n=2a$，消去 $ m$，$n$，得到 $3{a^2}={c^2}$，即得 $b=\sqrt 2a $．
题目
答案
解析
备注
