如图，设椭圆 $\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1 \left(a > b > 0\right) $ 的左、右焦点分别为 ${F_1}$，${F_2}$，点 $ D $ 在椭圆上，$D{F_1}\perp{F_1}{F_2}$，$\dfrac{{\big|{F_1}{F_2}\big|}}{{\big|D{F_1}\big|}}= 2\sqrt 2 $，$\triangle D{F_1}{F_2}$ 的面积为 $\dfrac{\sqrt 2 }{2}$．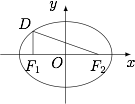
【难度】
【出处】
2014年高考重庆卷（理）
【标注】
-
求椭圆的标准方程；标注答案椭圆的标准方程为 $\dfrac{x^2}2+y^2=1$解析根据题意，由 $DF_1\perp F_1F_2$ 得 $\big|DF_1\big|=\dfrac{b^2}a$，进而有$$\begin{cases}2c=2\sqrt 2\cdot\dfrac{b^2}a,\\\dfrac 12\cdot 2c\cdot \dfrac{b^2}a =\dfrac{\sqrt 2}2,\\a^2=b^2+c^2,\end{cases}$$解得$$\begin{cases}a=\sqrt 2,\\b=1,\\c=1,\end{cases}$$因此椭圆的标准方程为 $\dfrac{x^2}2+y^2=1$．
-
设圆心在 $y$ 轴上的圆与椭圆在 $x$ 轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．标注答案$\dfrac{4\sqrt 2}3$解析如图，设圆心为 $P$，切点分别为 $A,B$，圆在 $A,B$ 处的切线分别为 $QA,QB$，其中 $Q$ 为两条切线的交点，则根据题意，$PA\perp AQ$，$PB\perp BQ$，$BQ\perp AQ$，$\big|PA\big|=\big|PB\big|$，因此四边形 $PAQB$ 为正方形．
由椭圆和圆的对称性可得直线 $AQ,BQ$ 的斜率分别为 $-1,1$，因此 $Q$ 为椭圆的下顶点，于是圆的半径就是过焦点的弦 $AQ$ 的长度．
连接 $AF_2$，设 $\big|AF_1\big|=m$，则 $\big|AF_2\big|=2\sqrt 2-m$，在直角三角形 $AQF_2$ 中，有$$\big|AQ\big|^2+\big|QF_2\big|^2=\big|AF_2\big|^2,$$即$$(\sqrt 2+m)^2+(\sqrt 2)^2=(2\sqrt 2-m)^2,$$解得 $m=\dfrac{\sqrt 2}3$．
因此所求半径的长为$$\big|AQ\big|=\big|QF_1\big|+\big|F_1A\big|=\dfrac{4\sqrt 2}3.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
