已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)所在平面内有一个不与原点重合的点 $P(x_0,y_0)$,过 $P$ 作 $E$ 的任意两条割线 $AB,CD$,其中 $A,B,C,D$ 均在椭圆 $E$ 上.证明:直线 $AC$ 和 $BD$ 的交点在定直线上.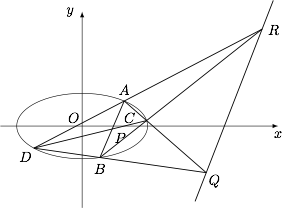

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
首先给出引理.
引理 过点 $P$ 的直线 $l$ 与椭圆交于 $S,T$ 两点,$X$ 为直线 $ST$ 上的点,那么 $P,X$ 调和分割 $S,T$,即“$\dfrac{|SX|}{|XT|}=\dfrac{|SP|}{|PT|}$”与“点 $X$ 在直线 $\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$ 上”等价.
该引理利用直线的参数方程或定比点差法容易证明,此处从略.
根据引理,我们只需要证明调和分割 $A,B$ 的点以及调和分割 $C,D$ 的点在直线 $RQ$ 上即可(完全四边形的性质).设 $AB,CD$ 与直线 $RQ$ 的交点分别为 $S,T$.事实上,对 $\triangle CDQ$ 和截线 $APB$ 应用梅涅劳斯定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CP|}{|PD|}=1,$$对于 $\triangle CDQ$ 和点 $R$ 应用塞瓦定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CT|}{|TD|}=1,$$于是 $\dfrac{|CP|}{|PD|}=\dfrac{|CT|}{|TD|}$,因此 $P,T$ 调和分割 $C,D$.类似的,有 $P,S$ 调和分割 $A,B$.因此原命题得证.
该引理利用直线的参数方程或定比点差法容易证明,此处从略.
根据引理,我们只需要证明调和分割 $A,B$ 的点以及调和分割 $C,D$ 的点在直线 $RQ$ 上即可(完全四边形的性质).设 $AB,CD$ 与直线 $RQ$ 的交点分别为 $S,T$.事实上,对 $\triangle CDQ$ 和截线 $APB$ 应用梅涅劳斯定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CP|}{|PD|}=1,$$对于 $\triangle CDQ$ 和点 $R$ 应用塞瓦定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CT|}{|TD|}=1,$$于是 $\dfrac{|CP|}{|PD|}=\dfrac{|CT|}{|TD|}$,因此 $P,T$ 调和分割 $C,D$.类似的,有 $P,S$ 调和分割 $A,B$.因此原命题得证.
答案
解析
备注