已知椭圆 $C:\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left(a > b > 0\right)$ 的一个焦点为 $\left(\sqrt 5 ,0\right)$，离心率为 $\dfrac{\sqrt 5 }{3}$．
【难度】
【出处】
2014年高考广东卷（文）
【标注】
-
求椭圆 $C$ 的标准方程；标注答案$\dfrac{x^2}9+\dfrac{y^2}4=1$解析记 $c$ 为椭圆的半焦距，则根据题意有 $c=\sqrt 5$，$\dfrac ca=\dfrac{\sqrt 5}3$，进而可得 $a=3$，$b=2$．因此椭圆 $C$ 的标准方程为 $\dfrac{x^2}9+\dfrac{y^2}4=1$．
-
若动点 $P\left({x_0},{y_0}\right)$ 为椭圆 $C$ 外一点，且点 $P$ 到椭圆 $C$ 的两条切线相互垂直，求点 $P$ 的轨迹方程．标注答案$x^2+y^2=13$解析当 $x_0\neq \pm 3$ 时，如图，设过 $P(x_0,y_0)$ 的椭圆 $C$ 的切线为 $y=k(x-x_0)+y_0$（$k\neq 0$）．
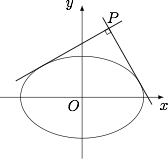由椭圆的等效判别式等于零得$$9k^2+4-(y_0-kx_0)^2=0,$$即$$(9-x_0^2)\cdot k^2+2x_0y_0\cdot k+4-y_0^2=0.$$根据题意，这个关于 $k$ 的方程的两根 $k_1,k_2$，即点 $P$ 到椭圆 $C$ 的两条切线的斜率，因此有 $k_1\cdot k_2=-1$，从而$$\dfrac{4-y_0^2}{9-x_0^2}=-1,$$即$$x_0^2+y_0^2=13(x_0\neq\pm 3).$$当 $x_0=\pm 3$ 时，$P$ 点的坐标为 $(3,\pm 2)$ 以及 $(-3,\pm 2)$，也符合上述方程．综上所述，所求轨迹方程为 $x^2+y^2=13$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
