在平面直角坐标系 $xOy$ 中，点 $M$ 到点 $F\left({1,0}\right)$ 的距离比它到 $y$ 轴的距离多 $ 1 $．记点 $M$ 的轨迹为 $C$．
【难度】
【出处】
2014年高考湖北卷（文）
【标注】
-
求轨迹 $C$ 的方程；标注答案轨迹 $C$ 的方程为 $y^2=\begin{cases} 4x,&x\geqslant 0,\\0,&x<0.\end{cases}$解析根据题意，设 $M(x,y)$，则$$\sqrt{(x-1)^2+y^2}=|x|+1,$$即 $y^2=2x+2|x|$．因此轨迹 $C$ 的方程为 $y^2=\begin{cases} 4x,&x\geqslant 0,\\0,&x<0.\end{cases}$
-
设斜率为 $k$ 的直线 $l$ 过定点 $P\left({-2,1}\right)$，求直线 $l$ 与轨迹 $C$ 恰好有一个公共点、两个公共点、三个公共点时 $k$ 的相应取值范围．标注答案直线 $l$ 与轨迹 $C$ 的公共点个数分别为 $1,2,3$ 时，对应的 $k$ 的取值范围是$$\begin{cases} (-\infty ,-1)\cup\{0\}\cup\left(\dfrac 12,+\infty \right),& 1\text{个公共点},\\
\{-1\}\cup\left[-\dfrac 12,0\right)\cup\left\{\dfrac 12\right\},& 2\text{ 个公共点},\\
\left(-1,-\dfrac 12\right)\cup\left(0,\dfrac 12\right),& 3\text{个公共点 }.\end{cases}$$解析如图，直线 $l_1,l_2$ 是抛物线 $y^2=4x$ 过点 $P(-2,1)$ 的两条切线，直线 $l_3$ 是过 $P$ 且与 $x$ 轴平行的直线，直线 $l_4$ 即直线 $OP$．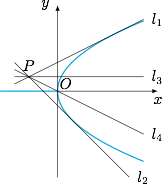
联立直线 $x+2=m(y-1)$（其中 $m$ 为斜率的倒数）与抛物线 $y^2=4x$ 可得$$y^2-4my+4m+8=0,$$于是由判别式为零得到方程$$m^2-m-2=0,$$解得直线 $l_1$ 的斜率为 $\dfrac 12$，直线 $l_2$ 的斜率为 $-1$，又直线 $l_3$ 的斜率为 $0$，直线 $l_4$ 的斜率为 $-\dfrac 12$．设直线 $l$ 与 $C_1:y=0$（$x<0$）的公共点个数为 $n_1$，与 $C_2:y^2=4x$ 的公共点个数为 $n_2$，则直线 $l$ 与轨迹 $C$ 的公共点个数 $n=n_1+n_2$，讨论如下．$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline
k & (-\infty,-1) & -1 & \left(-1,-\dfrac 12\right) & -\dfrac 12 & \left(-\dfrac 12,0\right) & 0 & \left(0,\dfrac 12\right) & \dfrac 12 & \left(\dfrac 12,+\infty \right)\\ \hline
n_1& 1 & 1 & 1& 0 & 0& 0 & 1 & 1 & 1\\ \hline
n_2& 0 & 1 & 2 & 2 & 2& 1 & 2 & 1 & 0\\ \hline
n& 1 & 2 & 3 & 2 & 2 & 1 & 3& 2 & 1\\ \hline
\end{array}$$因此直线 $l$ 与轨迹 $C$ 的公共点个数分别为 $1,2,3$ 时，对应的 $k$ 的取值范围是$$\begin{cases} (-\infty ,-1)\cup\{0\}\cup\left(\dfrac 12,+\infty \right),& 1\text{个公共点},\\
\{-1\}\cup\left[-\dfrac 12,0\right)\cup\left\{\dfrac 12\right\},& 2\text{ 个公共点},\\
\left(-1,-\dfrac 12\right)\cup\left(0,\dfrac 12\right),& 3\text{个公共点 }.\end{cases}$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
