三角形 $ABC$ 内接于圆 $\omega$，$P,Q$ 是线段 $AB$ 上的点，且 $AP<AQ$．射线 $CP,CQ$ 分别交圆 $\omega$ 于点 $S,T$．如果 $AP=4,PQ=3,QB=6,BT=5,AS=7$，设 $ST=\dfrac{m}{n}$，其中 $m,n$ 为互质的正整数．求 $m+n$ 的值．
【难度】
【出处】
2016年第34届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
$43$
【解析】
如图．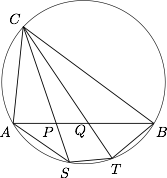
因为\[\begin{split}\dfrac{AP\cdot QB \cdot ST}{AS\cdot BT \cdot PQ}&=\dfrac{AP}{AS}\cdot \dfrac{QB}{BT}\cdot \dfrac{ST}{PQ} \\&= \dfrac{AP}{AS}\cdot \dfrac{QC}{CA}\cdot \dfrac{ST}{PQ} \\&=\dfrac{AP}{CA}\cdot \dfrac{QC}{PQ}\cdot \dfrac{ST}{AS}\\&=\dfrac{\sin \angle ACP}{\sin \angle APC}\cdot \dfrac{\sin \angle CPQ}{\sin \angle PCQ}\cdot \dfrac{\sin \angle PCQ}{\sin \angle ACP} \\&=1,\end{split}\]所以 $ST=\dfrac{35}{8}$．
另法 由射影几何中的Chasles定理可知，$$[CA,CT;CS,CB]=[A,T;S,B]=[A,Q;P,B],$$所以 $ST=\dfrac{35}{8}$．
因为\[\begin{split}\dfrac{AP\cdot QB \cdot ST}{AS\cdot BT \cdot PQ}&=\dfrac{AP}{AS}\cdot \dfrac{QB}{BT}\cdot \dfrac{ST}{PQ} \\&= \dfrac{AP}{AS}\cdot \dfrac{QC}{CA}\cdot \dfrac{ST}{PQ} \\&=\dfrac{AP}{CA}\cdot \dfrac{QC}{PQ}\cdot \dfrac{ST}{AS}\\&=\dfrac{\sin \angle ACP}{\sin \angle APC}\cdot \dfrac{\sin \angle CPQ}{\sin \angle PCQ}\cdot \dfrac{\sin \angle PCQ}{\sin \angle ACP} \\&=1,\end{split}\]所以 $ST=\dfrac{35}{8}$．
答案
解析
备注
