已知函数 $f\left(x\right) ={{\mathrm{e}}^x}+{{\mathrm{e}}^{- x}}$,其中 ${\mathrm{e}}$ 是自然对数的底数.
【难度】
【出处】
2014年高考江苏卷
【标注】
-
证明:$f\left(x\right)$ 是 ${\mathbb{R}}$ 上的偶函数;标注答案略解析函数 $f(x)$ 的定义域为 $\mathbb R$,对任意 $x\in{\mathbb R}$,有$$f(-x)={\rm e} ^{-x}+{\rm e} ^{x}=f(x),$$因此 $f(x)$ 是 $\mathbb R$ 上的偶函数.
-
若关于 $x$ 的不等式 $mf\left(x\right) \leqslant{{\mathrm{e}}^{- x}}+ m - 1$ 在 $\left(0, + \infty \right)$ 上恒成立,求实数 $m$ 的取值范围;标注答案$\left(-\infty ,-\dfrac 13\right]$解析根据题意,有$$\forall x\in(0,+\infty ),m\left({\rm e} ^{x}+{\rm e} ^{-x}\right)\leqslant {\rm e} ^{-x}+m-1,$$令 ${\rm e} ^x=t$,则$$\forall t>1,m\left(t+\dfrac 1t\right)\leqslant \dfrac 1t+m-1,$$即$$\forall t>1,m\leqslant \dfrac{1-t}{t^2-t+1},$$根据均值不等式,有$$\dfrac{1-t}{t^2-t+1}=-\dfrac{1}{t-1+\dfrac{1}{t-1}+1}\geqslant -\dfrac 13,$$等号当 $t=2$ 时取得.因此 $m$ 的取值范围是 $\left(-\infty ,-\dfrac 13\right]$.
-
已知正数 $a$ 满足:存在 ${x_0}\in \left[1 , + \infty \right)$,使得 $f\left({x_0}\right) < a\left( -x_0^3 + 3{x_0}\right)$ 成立.试比较 ${{\mathrm{e}}^{a - 1}}$ 与 ${a^{{\mathrm{e}}- 1}}$ 的大小,并证明你的结论.标注答案当 $a\in\left(\dfrac{{\rm e} +{\rm e} ^{-1}}2,{\rm e} \right)$ 时,${\rm e} ^{a-1}<a^{{\rm e} -1}$;当 $a={\rm e}$ 时,${\rm e}^{a-1}=a^{{\rm e} -1}$;当 $a\in\left({\rm e},+\infty \right)$ 时,${\rm e} ^{a-1}>a^{{\rm e} -1}$解析先确定 $a$ 的取值范围.根据题意有$$\exists x\geqslant 1,{\rm e} ^x+{\rm e} ^{-x}<a(-x^3+3x),$$即$$\exists x\geqslant 1,{\rm e} ^x+{\rm e} ^{-x}+ax^3-3ax<0,$$令上述命题中不等式左侧函数为 $g(x)$,则函数 $g(x)$ 的导函数$$g'(x)={\rm e} ^x-{\rm e} ^{-x}+3a(x^2-1),$$因此在区间 $[1,+\infty )$ 上,$g'(x)\geqslant 0$,因此 $g(x)$ 单调递增,于是由题意可知$$g(1)={\rm e} +{\rm e}^{-1} -2a<0,$$解得 $a>\dfrac{{\rm e} +{\rm e} ^{-1}}2$.
接下来比较 ${\rm e} ^{a-1}$ 与 $a^{{\rm e} -1}$ 的大小,只需要比较 $a-1$ 和 $({\rm e}-1)\ln a$ 的大小.记$$\varphi(a)=a-1-({\rm e}-1)\ln a,$$则其导函数$$\varphi'(a)=\dfrac {a-({\rm e}-1)}{a},$$因此在 $(0,{\rm e} -1)$ 上函数 $\varphi(a)$ 单调递减,在 $\left({\rm e} -1,+\infty \right)$ 上,函数 $\varphi(a)$ 单调递增,又注意到 $\varphi(1)=\varphi({\rm e} )=0$,因此当 $a\in\left(\dfrac{{\rm e} +{\rm e} ^{-1}}2,{\rm e} \right)$ 时,${\rm e} ^{a-1}<a^{{\rm e} -1}$;当 $a={\rm e}$ 时,${\rm e}^{a-1}=a^{{\rm e} -1}$;当 $a\in\left({\rm e},+\infty \right)$ 时,${\rm e} ^{a-1}>a^{{\rm e} -1}$.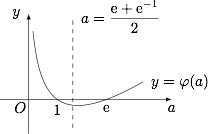
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3