设点 $A(1,0)$，$B(2,1)$，如果直线 $ax+by=1$ 与线段 $AB$ 有一个公共点，则 $a^2+b^2$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac{1}{5},+\infty\right)$
【解析】
题目中关键条件是直线 $ax+by=1$ 与线段 $AB$ 有一个公共点，这个条件可以转化成点 $A,B$ 在直线 $ax+by=1$ 的两侧或 $A,B$ 中有一点在直线 $ax+by=1$ 上（同时，直线不能与线段重合）．于是我们可以得到 $a$，$b$ 所满足的不等式，从而得到它们的可行域，再将所求代数式转化成可行域中的点 $(a,b)$ 到原点的距离的平方，考虑距离的最值即可．
因为线段 $AB$ 与直线有一个公共点，所以$$(a-1)(2a+b-1)\leqslant 0.$$建立平面直角坐标系 $aOb$，则 $a$，$b$ 所满足的可行域如图所示：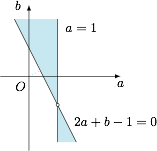
故原点到可行域中的点 $(a,b)$ 的距离 $\sqrt {a^2+b^2}$ 有最小值 $\dfrac{1}{\sqrt 5}$，从而 $a^2+b^2$ 有最小值 $\dfrac{1}{5}$．
因为线段 $AB$ 与直线有一个公共点，所以$$(a-1)(2a+b-1)\leqslant 0.$$建立平面直角坐标系 $aOb$，则 $a$，$b$ 所满足的可行域如图所示：
故原点到可行域中的点 $(a,b)$ 的距离 $\sqrt {a^2+b^2}$ 有最小值 $\dfrac{1}{\sqrt 5}$，从而 $a^2+b^2$ 有最小值 $\dfrac{1}{5}$．
答案
解析
备注
