在平面直角坐标系 $xOy$ 中,设 $\triangle ABC$ 的顶点分别为 $A(0,a)$,$B(b,0)$,$C(c,0)$,点 $P(0,p)$ 在线段 $AO$ 上(异于端点).设 $a,b,c,p$ 为非零常数,设直线 $BP,CP$ 分别与边 $AC,AB$ 交于点 $E,F$,求证:$\angle EOA=\angle FOA$.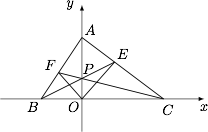

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
用截距式方程容易求得直线 $AC$ 与 $BP$ 的方程为$$AC:\dfrac xc+\dfrac ya=1,BP:\dfrac xb+\dfrac yp=1.$$所以过 $AC$ 与 $BP$ 的交点 $E$ 的直线系方程为$$\left(\dfrac xc+\dfrac ya-1\right)+\lambda\left(\dfrac xb+\dfrac yp-1\right)=0,$$其中 $\lambda$ 为参数.该直线过原点 $O(0,0)$,于是可得 $\lambda=-1$.因此直线 $OE$ 的方程为$$\left(\dfrac 1c-\dfrac 1b\right)x+\left(\dfrac 1a-\dfrac 1p\right)y=0.$$根据对称性可得直线 $OF$ 的方程为$$\left(\dfrac 1b-\dfrac 1c\right)x+\left(\dfrac 1a-\dfrac 1p\right)y=0,$$因此直线 $OE$ 与直线 $OF$ 斜率互为相反数,原命题得证.
答案
解析
备注