已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$),$AB,CD$ 是过椭圆左焦点 $F$ 的弦,且 $AB\perp CD$.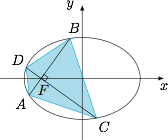

【难度】
【出处】
无
【标注】
-
求证:$\dfrac {1}{|AB|}+\dfrac {1}{|CD|}$ 为定值;标注答案略解析不妨直线 $AB$ 和 $CD$ 的倾斜角分别为 $\alpha$ 和 $\alpha+\dfrac{\pi}2$,椭圆的焦距为 $2c$,则根据椭圆的焦点弦长公式可得\[|AB|=\dfrac{2ab^2}{b^2+c^2\sin^2\alpha},|CD|=\dfrac{2ab^2}{b^2+c^2\cos^2\alpha}.\]根据题意,有\[\dfrac{1}{|AB|}+\dfrac{1}{|CD|}=\dfrac{b^2+c^2\sin^2\alpha}{2ab^2}+\dfrac{b^2+c^2\cos^2\alpha}{2ab^2}=\dfrac{2b^2+c^2}{2ab^2}=\dfrac{a^2+b^2}{2ab^2},
\]为定值. -
求 $A,B,C,D$ 构成的四边形的面积 $S$ 的取值范围.标注答案$\left[\dfrac{8a^2b^4}{(a^2+b^2)^2},2b^2\right]$解析根据题意,有\[S=\dfrac 12|AB|\cdot |CD|=\dfrac{2a^2b^4}{b^4+b^2c^2+\dfrac 14c^4\sin^22\alpha},\]于是 $S$ 的取值范围是 $\left[\dfrac{8a^2b^4}{(a^2+b^2)^2},2b^2\right]$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2