已知抛物线 $y^2=2px$($p>0$)的焦点 $F$ 和过焦点 $F$ 的弦 $AB$,过 $A,B$ 分别作抛物线的准线 $l$ 的垂线,垂足分别为 $D,C$.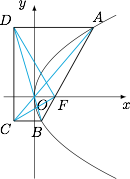
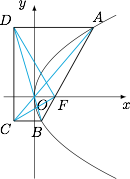
【难度】
【出处】
无
【标注】
-
求证:$FC\perp FD$;标注答案略解析根据抛物线的定义,有 $AF=AD$,$BF=BC$,于是\[\angle CFD=180^\circ-\angle AFD-\angle BFC=180^\circ-\dfrac{180^\circ-\angle DAF}2-\dfrac{180^\circ-\angle CBF}2=\dfrac{\angle DAF+\angle CBF}2=90^\circ.\]
-
求证:直角梯形 $ABCD$ 的对角线相交于坐标原点 $O$.标注答案略解析设 $AC,DC$ 分别与 $x$ 相交与点 $P,Q$,则\[\dfrac{FP}{BC}=\dfrac{AF}{AF+BF},\dfrac{PQ}{AD}=\dfrac{CP}{CA}=\dfrac{BF}{BF+AF},\]于是\[FP=PQ=\dfrac{AF\cdot BF}{AF+BF},\]因此 $P$ 点即 $O$ 点,原命题得证.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2