如图,曲线 $C$ 由上半椭圆 ${C_1}:\dfrac{y^2}{a^2}+ \dfrac{x^2}{b^2}= 1\left(a > b > 0,y \geqslant 0\right)$ 和部分抛物线 ${C_2}:y = -{x^2}+ 1\left(y \leqslant 0\right)$ 连接而成,${C_1}$ 与 ${C_2}$ 的公共点为 $A,B$,其中 ${C_1}$ 的离心率为 $\dfrac{\sqrt 3}{2}$.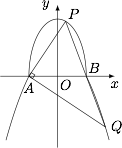

【难度】
【出处】
2014年高考陕西卷(理)
【标注】
-
求 $a,b$ 的值;标注答案$a,b$ 的值分别为 $2,1$解析由于 $A(-1,0)$,$B(1,0)$,因此 $b=1$.
又 $C_1$ 的离心率为 $\dfrac{\sqrt{a^2-b^2}}{a}=\dfrac{\sqrt 3}2$,因此解得 $a=2$.
综上,$a,b$ 的值分别为 $2,1$. -
过点 $B$ 的直线 $l$ 与 ${C_1},{C_2}$ 分别交于点 $P,Q$(均异于点 $A,B$),若 $AP \perp AQ$,求直线 $l$ 的方程.标注答案直线 $l$ 的方程为 $8x+3y-8=0$解析设直线 $PQ$ 的方程为 $l:x=my+1$,联立直线 $PQ$ 的方程与椭圆的方程,可得$$(4m^2+1)y^2+8my=0,$$因此 $P$ 点的纵坐标为 $y_1=-\dfrac{8m}{4m^2+1}$.
联立直线 $PQ$ 的方程与抛物线的方程,可得$$m^2y^2+(2m+1)y=0,$$因此 $Q$ 点的纵坐标为 $y_2=-\dfrac{2m+1}{m^2}$.
根据题意,有直线 $AP$ 与直线 $AQ$ 的斜率之积为 $-1$,即$$\dfrac{y_1-0}{my_1+1-(-1)}\cdot\dfrac{y_2-0}{my_2+1-(-1)}=-1,$$将 $y_1,y_2$ 关于 $m$ 的表达式代入,可得$$\dfrac{-\dfrac{8m}{4m^2+1}}{-\dfrac{8m^2}{4m^2+1}+2}\cdot\dfrac{-\dfrac{2m+1}{m^2}}{-\dfrac{2m+1}{m}+2}=-1,$$解得 $m=-\dfrac 38$,因此直线 $l$ 的方程为 $x=-\dfrac 38y+1$,即 $8x+3y-8=0$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2