已知椭圆 $C:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1 \left(a > b > 0 \right)$ 的焦距为 $4$,其短轴的两个端点与长轴的一个端点构成正三角形.
【难度】
【出处】
2014年高考四川卷(理)
【标注】
-
求椭圆 $C$ 的标准方程;标注答案椭圆 $C$ 的标准方程为 $\dfrac{x^2}6+\dfrac{y^2}2=1$解析根据题意,椭圆短轴的两个端点与长轴的一个端点构成正三角形,于是 $a=\dfrac{\sqrt 3}2\cdot 2b$,又 $2c=4$,$a^2=b^2+c^2$,因此可得 $a=\sqrt 6$,$b=\sqrt2$,所以椭圆 $C$ 的标准方程为 $\dfrac{x^2}6+\dfrac{y^2}2=1$.
-
设 $F$ 为椭圆 $C$ 的左焦点,$T$ 为直线 $x = - 3$ 上任意一点,过 $F$ 作 $TF$ 的垂线交椭圆 $C$ 于点 $P$,$Q$.
(i)证明:$OT$ 平分线段 $PQ$(其中 $O$ 为坐标原点);
(ii)当 $\dfrac{|TF|}{|PQ|}$ 最小时,求点 $T$ 的坐标.标注答案(i)略;(ii)$T$ 点的坐标为 $(-3,\pm 1)$解析设 $T(-3,t)$,$P(x_1,y_1)$,$Q(x_2,y_2)$,线段 $PQ$ 的中点为 $M$,连接 $OT$,如图.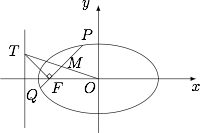 (i)
(i)情形一 $t\neq 0$.一方面,直线 $TF$ 的斜率为 $-t$,直线 $PQ$ 的斜率为 $\dfrac 1t$,直线 $OT$ 的斜率为 $-\dfrac t3$.
另一方面,由于 $\dfrac{x_1^2}6+\dfrac{y_1^2}2=1$,$\dfrac{x_2^2}6+\dfrac{y_2^2}2=1$,两式相减,并应用平方差公式可得$$\dfrac{(x_1+x_2)(x_1-x_2)}{6}+\dfrac{(y_1+y_2)(y_1-y_2)}{2}=0,$$从而$$\dfrac{y_1+y_2}{x_1+x_2}\cdot\dfrac{y_1-y_2}{x_1-x_2}=-\dfrac 13,$$即直线 $PQ$ 与直线 $OM$ 的斜率之积为 $-\dfrac 13$,进而直线 $OM$ 的斜率为 $-\dfrac t3$.
综合以上两方面,$O,M,T$ 三点共线,因此命题成立.情形二 $t=0$.此时 $OT$ 显然平分 $PQ$.
综上所述,命题得证.
(ii)直线 $PQ$ 的方程为 $x=ty-2$,与椭圆方程联立,有$$(t^2+3)y^2-4ty-2=0,$$因此\[\begin{split} \dfrac{|TF|}{|PQ|}&=\dfrac{\sqrt{t^2+1}}{\sqrt{1+t^2}\cdot\dfrac{\sqrt{24t^2+24}}{t^2+3}}\\
&=\dfrac{t^2+3}{\sqrt{24(t^2+1)}}\\
&=\sqrt{\dfrac 1{24}\cdot\left[(t^2+1)+\dfrac 4{t^2+1}+4\right]}\\
&\geqslant\sqrt{\dfrac{1}{3}},\end{split}\]等号当且仅当 $t^2+1=2$,即 $t=\pm 1$ 时取得.
因此当 $\dfrac{|TF|}{|PQ|}$ 最小时,$T$ 点的坐标为 $(-3,\pm 1)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2