函数 $y=x^2+ax+b$ 的图象与坐标轴交于三个不同的点 $A$、$B$、$C$,已知 $\triangle ABC$ 的外心在直线 $y=x$ 上,求 $a+b$ 的值.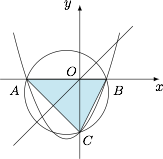

【难度】
【出处】
无
【标注】
【答案】
$ -1 $
【解析】
显然圆心的坐标为 $M \left( -\dfrac a2,-\dfrac a2\right) $,于是对原点 $O$ 应用圆幂定理有$$\overrightarrow {OA}\cdot \overrightarrow {OB}=OM^2-MC^2,$$即$$b=\left(-\dfrac a2\right)^2+\left(-\dfrac a2\right)^2-\left[\left(-\dfrac a2\right) ^2+ \left( -\dfrac a2-b\right)^2\right],$$整理即得$$a+b=-1.$$
答案
解析
备注