函数 $y=x^2+ax+b$ 的图象与坐标轴交于三个不同的点 $A$、$B$、$C$,已知 $\triangle ABC$ 的外心在直线 $y=x$ 上,求 $a+b$ 的值.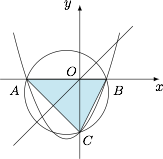

【难度】
【出处】
无
【标注】
【答案】
$ -1 $
【解析】
设 $A(x_1,0)$,$B(x_2,0)$,圆的方程为 $x^2+y^2+mx+my+n=0$,而 $C(0,b)$,于是$$\begin{cases} x_1^2+mx_1+n=0,\\x_2^2+mx_2+n=0,\\b^2+mb+n=0, \end{cases}$$由于 $x_1,x_2$ 同时是方程$$x^2+ax+b=0$$和方程$$x^2+mx+n=0$$的两个根,于是 $m=a$ 且 $n=b$,因此$$b^2+ab+b=0,$$即$$a+b=-1.$$
答案
解析
备注