已知函数 $f(x)=ax-{\rm e}^x$，若存在实数 $x$，使得 $f(x)\geqslant 0$，求 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$(-\infty,0)\cup [{\rm e},+\infty)$
【解析】
问题即$$\exists x\in\mathbb R,ax\geqslant {\rm e}^x,$$于是计算函数 $y={\rm e}^x$ 过原点的切线，作图如下：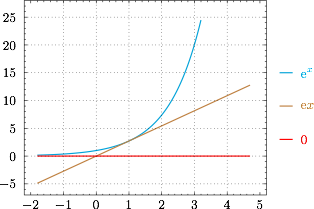
不难得到 $a$ 的取值范围是 $(-\infty,0)\cup [{\rm e},+\infty)$．
不难得到 $a$ 的取值范围是 $(-\infty,0)\cup [{\rm e},+\infty)$．
答案
解析
备注
