已知不等式 $x^2-2ax+2\geqslant a$ 对任意 $x \geqslant -1$ 都成立，求实数 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$[-3,1]$
【解析】
根据题意，有$$\forall x\in [-1,+\infty ),x^2-2ax+2\geqslant a,$$即$$\begin{cases} \forall x\in \left(-\dfrac 12,+\infty \right),a\leqslant \dfrac{x^2+2}{2x+1},\\\forall x\in\left[-1,-\dfrac 12\right),a \geqslant \dfrac{x^2+2}{2x+1},\end{cases}$$令 $t=2x+1$，则 $x=\dfrac 12(t-1)$，于是$$\dfrac{x^2+2}{2x+1}=\dfrac{t^2-2t+9}{4t}=\dfrac 14\left(t+\dfrac 9t-2\right),$$因此问题转化为$$\begin{cases} \forall t\in \left(0,+\infty \right),4a+2\leqslant t+\dfrac 9t,\\\forall t\in\left[-1,0\right),4a+2\geqslant t+\dfrac 9t,\end{cases}$$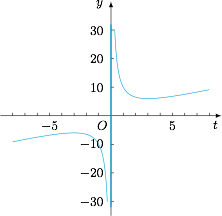
如图，结合对勾函数 $y=t+\dfrac 9t$ 的图象可得上式即$$4a+2 \leqslant 6\land 4a+2\geqslant -10,$$即$$-3\leqslant a\leqslant 1.$$综上，$a$ 的取值范围是 $[-3,1]$．
如图，结合对勾函数 $y=t+\dfrac 9t$ 的图象可得上式即$$4a+2 \leqslant 6\land 4a+2\geqslant -10,$$即$$-3\leqslant a\leqslant 1.$$综上，$a$ 的取值范围是 $[-3,1]$．
答案
解析
备注
