设 $a,b,c,d$ 都是正数，证明：存在三边分别等于 $\sqrt {b^2+c^2}$，$\sqrt{a^2+c^2+d^2+2cd}$，$\sqrt{a^2+b^2+d^2+2ab}$ 的三角形，并计算该三角形的面积．
【难度】
【出处】
2014年中国人民大学财经学院金融学与数学实验班选拔试题
【标注】
【答案】
$\dfrac 12(ac+bc+bd)$
【解析】
如图，阴影部分即为符合题意的三角形．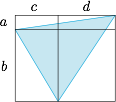
面积\[\begin{split}S_{ \triangle}&=(a+b)(c+d)-\dfrac 12\cdot a\cdot (c+d)-\dfrac 12\cdot bc-\dfrac 12\cdot d\cdot (a+b)\\&=\dfrac 12(ac+bc+bd).\end{split}\]
面积\[\begin{split}S_{ \triangle}&=(a+b)(c+d)-\dfrac 12\cdot a\cdot (c+d)-\dfrac 12\cdot bc-\dfrac 12\cdot d\cdot (a+b)\\&=\dfrac 12(ac+bc+bd).\end{split}\]
答案
解析
备注
