查看数据源：5955cb5dd3b4f9000ad5e8cf
设 $A,B,C$ 为边长为 $1$ 的三角形三边上各一点，求：$A{B^2} + B{C^2} + C{A^2}$ 的最小值．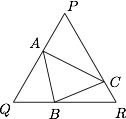
【难度】
【出处】
2012年北京大学等十三校联考自主招生
【标注】
  • 方法
    >
    代数处理
    >
    冻结变量法
  • 题型
    >
    不等式
    >
    求代数式的最值与范围
【答案】
$\dfrac{3}{4}$
【解析】
用冻结变量法解决该问题．令 $f = A{B^2} + B{C^2} + C{A^2}$．
第一步冻结 $A$、$B$．由于到 $A$、$B$ 距离平方之和为定值的点 $T$ 的轨迹为以 $AB$ 中点为圆心的圆，且 $T{A^2} + T{B^2}$ 越大，半径越大．于是当 $C$ 为从 $AB$ 的中点 $M$ 在 $PR$ 上的投影 $M'$ 时，$C{A^2} + C{B^2}$ 最小．
第二步冻结 $MM'$ 的值．此时 $C{A^2} + C{B^2}$ 的值不变，$M$ 在 $RP$ 的平行线 $l$ 上运动，考虑以 $M$ 为中点的线段 $AB$ 何时最小．
设 $l$ 与 $QP$、$QR$ 分别交与点 $E$、$F$，$QE = QF = a$，$QA = x$，则
由梅涅劳斯定理$$\dfrac{{AE}}{{EQ}} \cdot \dfrac{{QF}}{{FB}} \cdot \dfrac{{BM}}{{MA}} = 1,$$于是 $\dfrac{{x - a}}{a} \cdot \dfrac{a}{{a - QB}} = 1$，解得 $QB = 2a - x$．
因此\[\begin{split}A{B^2} &= Q{A^2} + Q{B^2} - QA \cdot QB \\&= {x^2} + {\left( {2a - x} \right)^2} - x\left( {2a - x} \right) \\&= 3{x^2} - 6ax + 4{a^2},\end{split}\]于是当且仅当 $x = a$ 时，$A{B^2}$ 最小为 ${a^2}$，也即当 $AB\parallel PR$ 时，$A{B^2}$ 最小．
第三步解冻 $MM'$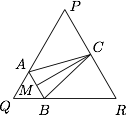．如图，设 $QA = QB = AB = x$，则\[\begin{split}A{B^2} + B{C^2} + C{A^2} &= {x^2} + 2\left[ {{{\left( {1 - x} \right)}^2} + \dfrac{1}{4} - \dfrac{1}{2}\left( {1 - x} \right)} \right] \\&= 3{x^2} - 3x + \dfrac{3}{2}\end{split}\]因此当 $x = \dfrac{1}{2}$ 时，$A{B^2} + B{C^2} + C{A^2}$ 最小，为 $\dfrac{3}{4}$．
答案 解析 备注
0.181057s