在平面直角坐标系 $xOy$ 中，设 $\triangle ABC$ 的顶点分别为 $A(0,a)$，$B(b,0)$，$C(c,0)$，点 $P(0,p)$ 在线段 $AO$ 上（异于端点）．设 $a,b,c,p$ 为非零常数，设直线 $BP,CP$ 分别与边 $AC,AB$ 交于点 $E,F$，求证：$\angle EOA=\angle FOA$．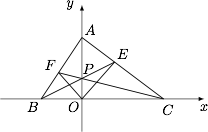
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
过 $A$ 作 $BC$ 的平行线 $l$，分别延长 $OE,OF$ 与 $l$ 相交于 $Q,R$，如图．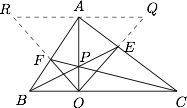
对 $\triangle ABC$ 应用塞瓦定理，有\[\dfrac{BO}{OC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}=1,\]又\[\dfrac{AR}{BO}=\dfrac{AF}{FB},\dfrac{AQ}{CO}=\dfrac{AE}{EC},\]于是 $AR=AQ$，进而 $\triangle ORQ$ 为等腰三角形，命题得证．
对 $\triangle ABC$ 应用塞瓦定理，有\[\dfrac{BO}{OC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}=1,\]又\[\dfrac{AR}{BO}=\dfrac{AF}{FB},\dfrac{AQ}{CO}=\dfrac{AE}{EC},\]于是 $AR=AQ$，进而 $\triangle ORQ$ 为等腰三角形，命题得证．
答案
解析
备注
