如图，在平面直角坐标系中，$P(6,8)$，四边形 $ABCD$ 为矩形，$AB=16$，$AD=9$，点 $A,B$ 分别在射线 $OP$ 和 $Ox$ 上，求 $OD$ 的最大值．
【难度】
【出处】
无
【标注】
【答案】
$27$
【解析】
注意到在矩形 $ABCD$ 运动的过程中 $\angle AOB$ 始终不变，因此可以看作矩形 $ABCD$ 不动，而点 $O$ 在圆弧上运动，如图．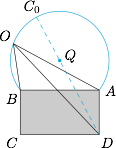
在图中，由于 $\tan\angle AOB=\dfrac 43$，于是 $Q$ 到弦 $AB$ 的距离为 $6$，圆 $Q$ 的半径为 $10$．因此 $OD$ 的最大值$$C_0D=C_0Q+QD=10+\sqrt{(6+9)^2+8^2}=27.$$
在图中，由于 $\tan\angle AOB=\dfrac 43$，于是 $Q$ 到弦 $AB$ 的距离为 $6$，圆 $Q$ 的半径为 $10$．因此 $OD$ 的最大值$$C_0D=C_0Q+QD=10+\sqrt{(6+9)^2+8^2}=27.$$
答案
解析
备注
