已知过点 $A(0,1)$ 且斜率为 $k$ 的直线 $l$ 与圆 $C:(x-2)^2+(y-3)^2=1$ 交于 $M,N$ 两点．
【难度】
【出处】
2015年高考全国Ⅰ卷（文）
【标注】
-
求 $k$ 的取值范围；标注答案$\left(\dfrac{4-\sqrt 7}3,\dfrac{4+\sqrt 7}3\right)$解析圆 $C$ 的圆心 $C(2,3)$ 到直线 $l:y=kx+1$ 的距离为$$\dfrac{|2k-2|}{\sqrt{1+k^2}}<1,$$解得$$\dfrac{4-\sqrt 7}3<k<\dfrac{4+\sqrt 7}3,$$于是 $k$ 的取值范围是 $\left(\dfrac{4-\sqrt 7}3,\dfrac{4+\sqrt 7}3\right)$．
-
若 $\overrightarrow{OM}\cdot \overrightarrow {ON}=12$，其中 $O$ 为坐标原点，求 $|MN|$．标注答案$2$解析根据题意$$\left(\overrightarrow {AM}-\overrightarrow {AO}\right)\cdot\left(\overrightarrow {AN}-\overrightarrow {AO}\right)=12,$$即$$\overrightarrow {AM}\cdot \overrightarrow {AN}-\overrightarrow {AO}\cdot\left(\overrightarrow {AM}+\overrightarrow {AN}\right) +\overrightarrow {AO}\cdot\overrightarrow {AO}=12.$$
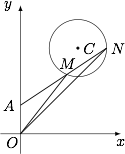由圆幂定理，得$$\overrightarrow {AM}\cdot\overrightarrow {AN}=AC^2-r^2=7,$$其中 $r$ 表示圆 $C$ 的半径．
取弦 $MN$ 的中点 $P$，则$$\overrightarrow {AM}+\overrightarrow {AN}=2\overrightarrow {AP},$$于是可得$$7- \overrightarrow {AO}\cdot 2\overrightarrow {AP}+1=12,$$化简得$$\overrightarrow {AO}\cdot \overrightarrow {AP}=-2,$$从而 $y_P=3$．
因此易知 $P$ 即圆 $C$ 的圆心，进而 $MN$ 为圆 $C$ 的直径，所求长度为 $2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
