如图，三棱锥 $P-ABC$ 中，$PA \perp$ 平面 $ABC$，$PA=1$，$AB=1$，$AC=2$，$\angle BAC=60^\circ$．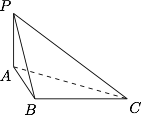
【难度】
【出处】
2015年高考安徽卷（文）
【标注】
-
求三棱锥 $P-ABC$ 的体积；标注答案$\dfrac {\sqrt 3}6$解析三棱锥 $P-ABC$ 的体积为$$\dfrac 13\cdot S_{\triangle ABC}\cdot PA=\dfrac 13\cdot \left(\dfrac 12\cdot AB\cdot AC\cdot \sin\angle BAC\right)\cdot PA=\dfrac {\sqrt 3}6.$$
-
证明：在线段 $PC$ 上存在点 $M$，使得 $AC\perp BM$，并求 $\dfrac{PM}{MC}$ 的值．标注答案$\dfrac{PM}{MC}=\dfrac 13$解析在底面 $ABC$ 内，过 $B$ 作 $AC$ 的垂线，垂足为 $H$，在三角形 $PAC$ 内，过 $H$ 作 $AC$ 的垂线与 $PC$ 相交，则交点即为所求的 $M$，证明如下．
因为 $MH\perp AC$，$BH\perp AC$，$MH$ 与 $BH$ 交于 $H$，所以 $AC\perp$ 平面 $MBH$，进而有 $AC\perp BM$．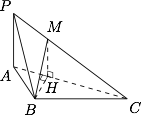
在 $\triangle PAC$ 中，由于 $MH\parallel PA$，于是$$\dfrac{PM}{MC}=\dfrac{AH}{HC}=\dfrac{AB\cdot \cos 60^\circ}{AC-AB\cdot \cos 60^\circ}=\dfrac 13.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
