已知点 $F$ 为抛物线 $E:y^2=2px$($p>0$)的焦点,点 $A(2,m)$ 在抛物线 $E$ 上,且 $|AF|=3$.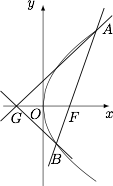

【难度】
【出处】
2015年高考福建卷(文)
【标注】
-
求抛物线 $E$ 的方程;标注答案$y^2=4x$解析根据抛物线的定义,有 $|AF|=2+\dfrac p2$,于是 $p=2$,所以抛物线 $E$ 的方程为 $y^2=4x$.
-
已知点 $G(-1,0)$,延长 $AF$ 交抛物线 $E$ 于点 $B$,证明:以点 $F$ 为圆心且与直线 $GA$ 相切的圆,必与直线 $GB$ 相切.标注答案略解析条件“以点 $F$ 为圆心且与直线 $GA$ 相切的圆同时与直线 $GB$ 相切”等价于“直线 $AG$ 与直线 $BG$ 的斜率互为相反数”.
根据题意,有 $A(2,2\sqrt2)$,$F(1,0)$,因此 $AB:y=2\sqrt 2(x-1)$.
联立直线 $AB$ 的方程与抛物线方程可得 $B\left(\dfrac 12,-\sqrt 2\right)$,于是 $AG$ 的斜率与 $BG$ 的斜率之和为$$\dfrac{2\sqrt 2-0}{2-(-1)}+\dfrac{-\sqrt 2-0}{\dfrac 12-(-1)}=0,$$因此命题得证.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2