为测量一工件的内圆弧半径 $R$，工人用三个半径均为 $r$ 的圆柱形量棒 ${O_1},{O_2},{O_3}$ 放在与工件圆弧相切的位置上，如图．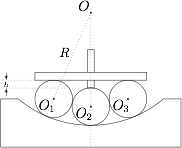
通过深度卡尺测出卡尺水平面到中间量棒 ${O_2}$ 顶侧面的垂直深度 $h$，试写出 $R$ 用 $h$ 表示的函数关系式，并计算当 $r = 10$ $\rm{mm}$，$h = 4$ $\rm{mm}$ 时，$R$ 的值．
通过深度卡尺测出卡尺水平面到中间量棒 ${O_2}$ 顶侧面的垂直深度 $h$，试写出 $R$ 用 $h$ 表示的函数关系式，并计算当 $r = 10$ $\rm{mm}$，$h = 4$ $\rm{mm}$ 时，$R$ 的值．【难度】
【出处】
2007年上海交通大学冬令营选拔测试
【标注】
【答案】
$60$
【解析】
如图，
$$h = OB - OH,$$而$$OA = OB = OC = R - r.$$设$$\angle AOM = \angle MOB = \angle BON = \angle NOC = \theta ,$$于是$$OH = \cos 2\theta \cdot OA,$$所以\[h= OA\left( {1 - \cos 2\theta } \right) = OA \cdot 2{\sin ^2}\theta = 2\left( {R - r} \right){\sin ^2}\theta .\]而$$\sin \theta = \dfrac{r}{{R - r}},$$所以$$h = 2\left( {R - r} \right) \cdot \dfrac{{{r^2}}}{{{{\left( {R - r} \right)}^2}}} = \dfrac{{2{r^2}}}{{R - r}}.$$因此$$R = \dfrac{{2{r^2}}}{h} + r.$$所以当 $r = 10$，$h = 4$ 时，$R = 60$ ${\mathrm{mm}}$．
$$h = OB - OH,$$而$$OA = OB = OC = R - r.$$设$$\angle AOM = \angle MOB = \angle BON = \angle NOC = \theta ,$$于是$$OH = \cos 2\theta \cdot OA,$$所以\[h= OA\left( {1 - \cos 2\theta } \right) = OA \cdot 2{\sin ^2}\theta = 2\left( {R - r} \right){\sin ^2}\theta .\]而$$\sin \theta = \dfrac{r}{{R - r}},$$所以$$h = 2\left( {R - r} \right) \cdot \dfrac{{{r^2}}}{{{{\left( {R - r} \right)}^2}}} = \dfrac{{2{r^2}}}{{R - r}}.$$因此$$R = \dfrac{{2{r^2}}}{h} + r.$$所以当 $r = 10$，$h = 4$ 时，$R = 60$ ${\mathrm{mm}}$．
答案
解析
备注
