一艘船以 ${v_1} = 10\rm {{km}}/{{h}}$ 向西行驶，在西南方向 $300 \rm {{km}}$ 处有一台风中心，周围 $100 \rm {{km}}$ 为暴雨区，且以 ${v_2} = 20 \rm {{km/h}}$ 向北移动，问该船遭遇暴雨的时间段长度．
【难度】
【出处】
2002年复旦大学保送生招生测试
【标注】
【答案】
$2\sqrt 2 $ 小时
【解析】
遭遇暴雨即台风中心到船的距离不超过 $100 \rm {{km}}$，建立直角坐标系如图．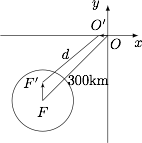
设船行驶了 $t$ 小时，则船的坐标为 $\left( { - 10t , 0} \right)$，台风中心的坐标为 $\left( { - 150\sqrt 2, - 150\sqrt 2 + 20t} \right)$．
船与台风中心的距离$$d = \sqrt {{{\left( {150\sqrt 2 - 10t} \right)}^2} + {{\left( {150\sqrt 2 - 20t} \right)}^2}} \leqslant 100,$$化简得 ${t^2} - 18\sqrt 2 t + 160 \leqslant 0$，解得 $8\sqrt 2 \leqslant t \leqslant 10\sqrt 2 $．
设船行驶了 $t$ 小时，则船的坐标为 $\left( { - 10t , 0} \right)$，台风中心的坐标为 $\left( { - 150\sqrt 2, - 150\sqrt 2 + 20t} \right)$．船与台风中心的距离$$d = \sqrt {{{\left( {150\sqrt 2 - 10t} \right)}^2} + {{\left( {150\sqrt 2 - 20t} \right)}^2}} \leqslant 100,$$化简得 ${t^2} - 18\sqrt 2 t + 160 \leqslant 0$，解得 $8\sqrt 2 \leqslant t \leqslant 10\sqrt 2 $．
答案
解析
备注
