有一四个顶点都在三角形 $ABC$ 三边上的内接正方形．已知 $\triangle ABC$ 为锐角三角形，三边长 $a,b,c$ 满足 $a > b > c$，求证：这个三角形的最大内接正方形边长为 $\dfrac{{ac\sin B}}{{c + a\sin B}}$．
【难度】
【出处】
2012年北京大学保送生试题
【标注】
【答案】
略
【解析】
如图所示，设正方形 $MNPQ$ 的边长为 $x$．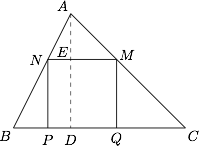
因为 $\dfrac{{AE}}{{AD}} = \dfrac{{MN}}{{BC}}$，所以$$\dfrac{{c\sin B - x}}{{c\sin B}} = \dfrac{x}{a},$$所以 $x =\dfrac {ac\sin B}{a+c\sin B}= \dfrac{{abc}}{{2Ra + bc}}$．
同理可得其它两种情况下内接正方形边长为 $\dfrac{{abc}}{{2Rb + ca}}$，$\dfrac{{abc}}{{2Rc + ab}}$．
因为\[\begin{split}&2Rb + ca - \left( {2Ra + bc} \right) = \left( {b - a} \right)\left( {2R - c} \right) < 0,\\& 2Rc + ab - \left( {2Rb + ca} \right) = \left( {c - b} \right)\left( {2R - a} \right) < 0.\end{split}\]所以这个三角形的内接正方形边长的最大值为 $\dfrac {abc}{2Rc+ab}=\dfrac{{ac\sin B}}{{c + a\sin B}}$．
因为 $\dfrac{{AE}}{{AD}} = \dfrac{{MN}}{{BC}}$，所以$$\dfrac{{c\sin B - x}}{{c\sin B}} = \dfrac{x}{a},$$所以 $x =\dfrac {ac\sin B}{a+c\sin B}= \dfrac{{abc}}{{2Ra + bc}}$．同理可得其它两种情况下内接正方形边长为 $\dfrac{{abc}}{{2Rb + ca}}$，$\dfrac{{abc}}{{2Rc + ab}}$．
因为\[\begin{split}&2Rb + ca - \left( {2Ra + bc} \right) = \left( {b - a} \right)\left( {2R - c} \right) < 0,\\& 2Rc + ab - \left( {2Rb + ca} \right) = \left( {c - b} \right)\left( {2R - a} \right) < 0.\end{split}\]所以这个三角形的内接正方形边长的最大值为 $\dfrac {abc}{2Rc+ab}=\dfrac{{ac\sin B}}{{c + a\sin B}}$．
答案
解析
备注
