如图,四面体 $ABCD$ 中,$O,E$ 分别是 $BD,BC$ 的中点,$AO$ 垂直于平面 $BCD$,且 $CA = CB = CD = 2$,$AB = \sqrt 2 $,求异面直线 $AB$ 与 $ED$ 所成角的大小.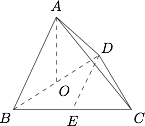

【难度】
【出处】
2008年上海财经大学自主招生试题
【标注】
【答案】
$\arccos \dfrac{{\sqrt 6 }}{4}$
【解析】
根据题意,有$$OA=OB=OD=1,$$且 $AB=AD=\sqrt 2$.而 $BE=1$,$AE=\sqrt 2$,$DE=\sqrt 3$,利用空间余弦定理,可得\[\begin{split}\cos\langle AB,ED\rangle &=\dfrac{\left|AD^2+BE^2-AE^2-BD^2\right|}{2\cdot AB\cdot DE}\\ &=\dfrac{|2+1-2-4|}{2\cdot \sqrt 2\cdot \sqrt 3} \\&=\dfrac{\sqrt 6}4.\end{split}\]
答案
解析
备注