如图，在四棱锥 $P - ABCD$ 中，底面 $ABCD$ 是直角梯形，$AD\parallel BC$，$AB \perp BC$，侧面 $PAB \perp $ 底面 $ABCD$，$PA=AD=AB=1$，$BC=2$．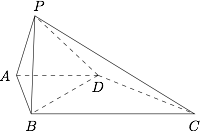
【难度】
【出处】
2012年卓越人才培养合作高校自主选拔学业能力测试数学试题
【标注】
-
证明：平面 $PBC \perp $ 平面 $PDC$．标注答案略解析延长 $BA$，$CD$，使其相交于点 $F$，连接 $PF$．
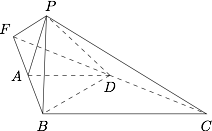容易知道，$AD$ 为 $\triangle FBC$ 的中位线，于是有$$PA = AF = AB = 1,\angle FPB = \dfrac{{{\pi }}}{2},$$即 $PF \perp PB$．
而 $BC \perp AB$，面 $PFB \perp $ 面 $ABC$，知 $BC \perp $ 面 $PFB$．而 $PF \subset $ 面 $PFB$，有 $PF \perp BC$．
于是 $PF \perp $ 面 $PBC$．$$\begin{cases}
PF \perp PBC ,\\
PF \subset PDC ,\\
\end{cases}\Rightarrow PBC \perp PDC.$$ -
若 $\angle PAB = {120^ \circ }$，求二面角 $B - PD - C$ 的正切值．标注答案$\dfrac{{4\sqrt 6 }}{3}$解析过点 $B$ 作 $BQ \perp PD$ 交 $PD$ 于 $Q$，过点 $B$ 作 $BH \perp PC$ 交 $PC$ 于 $H$，连接 $QH$．
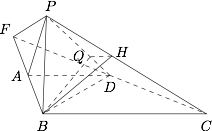由面 $PBC \perp $ 面 $PDC$，知 $\angle BQH$ 即为二面角 $B - PD - C$ 的平面角，$\tan \angle PQH = \dfrac{{BH}}{{QH}}$．
下面来求解 $BH,HQ,BQ$ 的值．
容易知道$$PF = PA = AF = AB = 1,PB = \sqrt 3 ,BC = 2.$$在 ${\mathrm {Rt}}\triangle PBC$ 中容易解得斜边上的高 $BH = \dfrac{{2\sqrt 3 }}{{\sqrt 7 }}$．$$PD = \sqrt {P{A^2} + A{Q^2}} = \sqrt 2 ,PB = \sqrt 3 ,BD = \sqrt 2. $$在 $\triangle PBD$ 中容易解得 $BQ = \dfrac{{\sqrt {15} }}{{2\sqrt 2 }}$．
而 $\triangle BHQ$ 为直角三角形，于是$$QH = \sqrt {B{Q^2} - B{H^2}} = \dfrac{3}{{2\sqrt {14} }},$$所以$$\tan \angle PQH = \dfrac{{BH}}{{QH}} = \dfrac{{4\sqrt 6 }}{3}.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
