如图所示,$\angle ACL=\angle BCL=\angle CBL=\angle BAL$.求证:$\triangle ABC$ 的三边长成等比数列.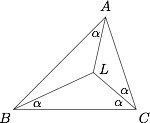

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
根据题意有$$\angle ALC = B+C,\angle CLB = B + A,\angle BLA = A + C,$$从而$$\dfrac{{AB}}{{\sin \angle ALB}}=\dfrac{{BL}}{{\sin \angle LAB}} = \dfrac{{BL}}{{\sin \angle BCL}} = \dfrac{{BC}}{{\sin \angle BLC}},$$因此 $\dfrac{{AB}}{{\sin \angle ALB}} = \dfrac{{BC}}{{\sin \angle BLC}}$,即 $\dfrac{{AB}}{{\sin B}} = \dfrac{{BC}}{{\sin {C} }}$,也即 $AC \cdot BC = AB{^2}$.
答案
解析
备注