设平面上有三个点，任意两个点之间的距离不超过 $1$．问：半径至少为多大的圆盘才能盖住这三个点．请证明你的结论．
【难度】
【出处】
2000年复旦大学保送生招生测试
【标注】
【答案】
$\dfrac{{\sqrt 3 }}{3}$
【解析】
半径 $r$ 至少为 $\dfrac{{\sqrt 3 }}{3}$．
不妨设平面上的三个点为 $A$、$B$、$C$．
先证明 $r \geqslant \dfrac{{\sqrt 3 }}{3}$，当 $\triangle ABC$ 是边长为 $1$ 的正三角形时，由于外接圆半径为 $\dfrac{{\sqrt 3 }}{3}$，
所以 $r \geqslant \dfrac{{\sqrt 3 }}{3}$；
再证明 $r = \dfrac{{\sqrt 3 }}{3}$ 时可以满足题意．
如图．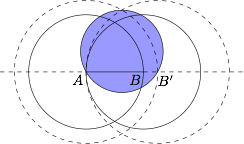
不妨设$$1 \geqslant AB \geqslant BC \geqslant CA,$$延长线段 $AB$ 到 $B'$ 使得 $AB'=1$（若 $AB = 1$，则 $B' = B$），则点 $C$ 在线段 $AB$ 上或在直线 $AB$ 一侧．
若点 $C$ 在线段 $AB$ 上，由于 $\dfrac{{\sqrt 3 }}{3} > \dfrac{{AB'}}{2}$，所以符合题意；
若点 $C$ 在直线 $AB$ 一侧，那么作半径为 $\dfrac{{\sqrt 3 }}{3}$ 的圆 $M$，使得点 $A$、$B'$ 在圆 $M$ 上，且 $M$ 与 $C$ 在直线 $AB$ 的同侧．
分别以点 $A$、$B$ 为圆心，$AB$ 为半径作圆．
设这两个圆的公共区域在点 $C$ 那侧部分为 $\Gamma $．
容易证明，$\Gamma $ 在圆 $M$ 内部（或者边界）．
综上，半径至少为 $\dfrac{{\sqrt 3 }}{3}$ 才能满足条件．
不妨设平面上的三个点为 $A$、$B$、$C$．
先证明 $r \geqslant \dfrac{{\sqrt 3 }}{3}$，当 $\triangle ABC$ 是边长为 $1$ 的正三角形时，由于外接圆半径为 $\dfrac{{\sqrt 3 }}{3}$，
所以 $r \geqslant \dfrac{{\sqrt 3 }}{3}$；
再证明 $r = \dfrac{{\sqrt 3 }}{3}$ 时可以满足题意．
如图．
不妨设$$1 \geqslant AB \geqslant BC \geqslant CA,$$延长线段 $AB$ 到 $B'$ 使得 $AB'=1$（若 $AB = 1$，则 $B' = B$），则点 $C$ 在线段 $AB$ 上或在直线 $AB$ 一侧．若点 $C$ 在线段 $AB$ 上，由于 $\dfrac{{\sqrt 3 }}{3} > \dfrac{{AB'}}{2}$，所以符合题意；
若点 $C$ 在直线 $AB$ 一侧，那么作半径为 $\dfrac{{\sqrt 3 }}{3}$ 的圆 $M$，使得点 $A$、$B'$ 在圆 $M$ 上，且 $M$ 与 $C$ 在直线 $AB$ 的同侧．
分别以点 $A$、$B$ 为圆心，$AB$ 为半径作圆．
设这两个圆的公共区域在点 $C$ 那侧部分为 $\Gamma $．
容易证明，$\Gamma $ 在圆 $M$ 内部（或者边界）．
综上，半径至少为 $\dfrac{{\sqrt 3 }}{3}$ 才能满足条件．
答案
解析
备注
