已知在正方体 $ABCD-A_1B_1C_1D_1$ 中，$O,E,F,G$ 分别为 $BD,BB_1,A_1D_1,D_1C_1$ 的中点，且 $AB=1$．求四面体 $OEFG$ 的体积．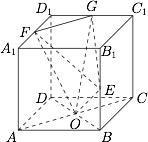
【难度】
【出处】
2011年全国高中数学联赛山东省预赛
【标注】
【答案】
$\dfrac 5{48}$
【解析】
连结 $B_1D_1$ 交 $FG$ 于 $H$，连结 $A_1C_1$，则 $B_1D_1\perp A_1C_1$．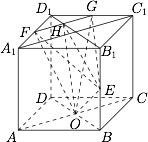
因为 $F,G$ 分别为 $A_1D_1,D_1C_1$ 的中点，所以$$FG\parallel A_1C_1,$$因此$$FG\perp B_1D_1.$$因为 $BB_1\perp $ 平面 $A_1B_1C_1D_1$，$FG$ 在平面 $A_1B_1C_1D_1$ 内，所以$$BB_1\perp FG.$$由此得 $FG\perp$ 面 $BB_1D_1D$．
因为 $FH=GH$，所以$$\begin{split}V_{O-EFG}&=V_{F-OEH}+V_{G-OEH}\\ &=2V_{F-OEH}=\dfrac 23 S_{OEH}\cdot FH.\end{split}$$在梯形 $OBB_1H$ 中，\[\begin{split}S_{\triangle{OEH}}&=S_{\text{梯形}OBB_1H}-S_{\triangle{EB_1H}}-S_{\triangle{OBE}}\\&=\dfrac{5\sqrt 2}{8}-\dfrac{\sqrt 2}{8}-\dfrac{3\sqrt 2}{16}\\&=\dfrac{5\sqrt 2}{16}.\end{split}\]因此四面体 $OEFG$ 的体积为$$V_{O-EFG}=2\times \dfrac 13 \times \dfrac{5\sqrt 2}{16}\times \dfrac{\sqrt 2}{4}=\dfrac 5{48}.$$
因为 $F,G$ 分别为 $A_1D_1,D_1C_1$ 的中点，所以$$FG\parallel A_1C_1,$$因此$$FG\perp B_1D_1.$$因为 $BB_1\perp $ 平面 $A_1B_1C_1D_1$，$FG$ 在平面 $A_1B_1C_1D_1$ 内，所以$$BB_1\perp FG.$$由此得 $FG\perp$ 面 $BB_1D_1D$．因为 $FH=GH$，所以$$\begin{split}V_{O-EFG}&=V_{F-OEH}+V_{G-OEH}\\ &=2V_{F-OEH}=\dfrac 23 S_{OEH}\cdot FH.\end{split}$$在梯形 $OBB_1H$ 中，\[\begin{split}S_{\triangle{OEH}}&=S_{\text{梯形}OBB_1H}-S_{\triangle{EB_1H}}-S_{\triangle{OBE}}\\&=\dfrac{5\sqrt 2}{8}-\dfrac{\sqrt 2}{8}-\dfrac{3\sqrt 2}{16}\\&=\dfrac{5\sqrt 2}{16}.\end{split}\]因此四面体 $OEFG$ 的体积为$$V_{O-EFG}=2\times \dfrac 13 \times \dfrac{5\sqrt 2}{16}\times \dfrac{\sqrt 2}{4}=\dfrac 5{48}.$$
答案
解析
备注
