如图,设锐角 $\triangle{ABC}$ 的外接圆为圆 $O$,过点 $B,C$ 作圆 $O$ 的两条切线,相交于点 $P$.连结 $AP$ 交 $BC$ 于点 $D$,点 $E,F$ 分别在边 $AC,AB$ 上,使得 $DE\parallel BA$,$DF\parallel CA$.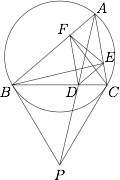 求证:
求证:
 求证:
求证:【难度】
【出处】
2011年全国高中数学联赛福建省预赛
【标注】
-
$\dfrac{BD}{CD}=\dfrac{AB^2}{AC^2}$;标注答案略解析设 $PA$ 交圆 $O$ 于另一点 $M$,连接 $BM,CM$.
由 $PB,PC$ 为圆 $O$ 的切线知,$$PB=PC,\angle{PBM=\angle{PAB}},\angle{PCM}=\angle{PAC},$$所以$$\triangle{PBM}\cong \triangle{PAB},\triangle{PCM}\cong \triangle{PAC}.$$因此$$\dfrac{BM}{AB}=\dfrac{PB}{PA},\dfrac{PC}{PA}=\dfrac{CM}{AC},$$即$$\dfrac{BM}{CM}=\dfrac{AB}{AC}.$$又 $\triangle{BDM}\backsim \triangle{ADC}$,$\triangle{CDM}\backsim \triangle{ADB}$,所以$$\dfrac{BM}{AC}=\dfrac{MD}{CD},\dfrac{AB}{CM}=\dfrac{BD}{MD}.$$因此$$\dfrac{BM}{AC}\cdot \dfrac{AB}{CM}=\dfrac{MD}{CD}\cdot \dfrac{BD}{MD},$$即$$\dfrac{BD}{CD}=\dfrac{BM}{CM}\cdot \dfrac{AB}{AC},$$故$$\dfrac{BD}{CD}=\dfrac{AB^2}{AC^2}.$$ -
$\angle{BCF}=\angle{BEF}$.标注答案略解析因为$$DE\parallel BA,DF\parallel CA,$$所以四边形 $AEDF$ 为平行四边形,从而$$AF=DE,AE=FD,\dfrac{ED}{AB}=\dfrac{CD}{CB},\dfrac{FD}{AC}=\dfrac{BD}{BC}.$$所以\[\begin{split}&AF=DE=\dfrac{AB\times CD}{BC},\\&AE=FD=\dfrac{AC\times BD}{BC},\end{split}\]因此\[\begin{split}&AE\times AB=\dfrac{AB^2\times CD}{BC},\\&AE\times AC=\dfrac{AC^2\times BD}{BC}.\end{split}\]又由 $\dfrac{BD}{CD}=\dfrac{AB^2}{AC^2}$ 知,$$BD=\dfrac{AB^2}{AC^2}\times CD,$$所以\[\begin{split}AE\times AC&=\dfrac{AC^2\times BD}{BC}\\&=\dfrac{AC^2}{BC}\times \dfrac{AB^2}{AC^2}\times CD\\&=\dfrac{AB^2\times CD}{BC}\\&=AF\times AB.\end{split}\]因此 $F,B,C,E$ 四点共圆,故 $\angle{BCF}=\angle{BEF}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2