已知 $P_1,P_2,P_3,\cdots ,P_{35}$ 是平面内凸三十五边形的 $35$ 个顶点，且 $P_1,P_2,P_3,\cdots ,P_{35}$ 中任何两点之间的距离不小于 $\sqrt 3$．求证：从这 $35$ 个点中可以选出 $5$ 个点，使得这 $5$ 个点中任意两点之间的距离不小于 $3$．
【难度】
【出处】
2011年全国高中数学联赛福建省预赛
【标注】
【答案】
略
【解析】
先证一个引理：设在 $P_1,P_2,P_3,\cdots ,P_{35}$ 这 $35$ 个点中任取一点，则在余下的 $34$ 个点中，至多有 $6$ 个点与 $P$ 点的距离小于 $3$．
（用反证法）如图，假设有 $7$ 个点，不妨设为 $P_1,P_2,P_3,\cdots ,P_7$（$P_1,P_2,P_3,\cdots ,P_7$ 按逆时针排列）与点 $P$ 的距离小于 $3$．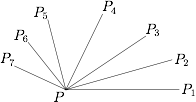
由 $P_1,P_2,P_3,\cdots ,P_{35}$ 是平面内凸三十五边形的 $35$ 个顶点知，$$\angle{P_1PP_2}+\angle{P_2PP_3}+\angle{P_3PP_4}+\angle{P_4PP_5}+\angle{P_5PP_6}+\angle{P_6PP_7}\leqslant 180^{\circ}.$$所以 $\angle{P_1PP_2}$，$\angle{P_2PP_3}$，$\angle{P_3PP_4}$，$\angle{P_4PP_5}$，$\angle{P_5PP_6}$，$\angle{P_6PP_7}$ 这 $6$ 个分角中至少有一个不大于 $30^{\circ}$，不妨设 $\angle{P_1PP_2}\leqslant 30^{\circ}$．
设 $PP_1=x$，$PP_2=y$，则\[\begin{split}P_1P_2^2&=x^2+y^2-2xy\cos {\angle{P_1PP_2}}\\&\leqslant x^2+y^2-2xy\cos{30^{\circ}}\\&=x^2+y^2-\sqrt 3 xy.\end{split}\]根据对称性，不妨设 $x\geqslant y$，由于$$\sqrt 3\leqslant y\leqslant x<3,$$所以$$P_1P_2^2=f(x)=x^2+y^2-\sqrt 3 xy=\left(x-\dfrac{\sqrt 3}{2}y\right)^2+\dfrac 14 y^2$$在区间 $[y,3)$ 上为增函数，因此\[\begin{split}P_1P_2^2&=f(x)<f(3)\\&=9+y^2-3\sqrt 3 y\\&=\left(y-\dfrac{3\sqrt 3}{2}\right)^2+\dfrac 94\\& \leqslant \left(\sqrt 3-\dfrac{3\sqrt 3}{2}\right)^2+\dfrac 34\\&=3,\end{split}\]而 $P_1P_2<\sqrt 3$ 与条件矛盾，因此假设不成立，所以引理得证．
下面利用引理证明本题结论．
根据引理，从 $P_1$ 出发的 $34$ 条线段 $P_1P_2$，$P_1P_3$，$P_1P_4$，$\cdots $，$P_1P_{35}$ 中至多有 $6$ 条线段的长度小于 $3$，即至少有 $28$ 条线段的长度不小于 $3$，不妨设线段 $P_1P_2,P_1P_3,P_1P_4,\cdots P_1P_{29}$ 的长度不小于 $3$．
再考察从 $P_2$ 出发的 $27$ 条线段 $P_2P_3,P_2P_4,P_2P_5,\cdots ,P_2P_{23}$，根据引理，这 $27$ 条线段中至多有 $6$ 条线段的长度小于 $3$，即至少有 $21$ 条线段的长度不小于 $3$，不妨设线段 $P_2P_3,P_2P_4,P_2P_5,\cdots ,P_2P_{24}$ 的长度不小于 $3$．
再考察从 $P_3$ 出发的 $20$ 条线段 $P_3P_4,P_3P_5,P_3P_6\cdots ,P_3P_{23}$，根据引理，这 $20$ 条线段中至多有 $6$ 条线段的长度小于 $3$，即至少有 $14$ 条线段的长度不小于 $3$，不妨设线段 $P_3P_4,P_3P_5,P_3P_6,\cdots ,P_3P_{17}$ 的长度不小于 $3$．
再考察从 $P_4$ 出发的 $13$ 条线段 $P_4P_5,P_4P_6,P_4P_7,\cdots ,P_4P_{17}$，根据引理，这 $13$ 条线段中至多有 $6$ 条线段的长度小于 $3$，至少有 $7$ 条线段的长度不小于 $3$，不妨设线段 $P_4P_5,P_4P_6,P_4P_7,\cdots ,P_4P_{11}$ 的长度不小于 $3$．
这样得到 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$，根据前面的讨论，这 $5$ 个点中任意两点之间的距离不小于 $3$．
所以，结论成立．
（用反证法）如图，假设有 $7$ 个点，不妨设为 $P_1,P_2,P_3,\cdots ,P_7$（$P_1,P_2,P_3,\cdots ,P_7$ 按逆时针排列）与点 $P$ 的距离小于 $3$．
由 $P_1,P_2,P_3,\cdots ,P_{35}$ 是平面内凸三十五边形的 $35$ 个顶点知，$$\angle{P_1PP_2}+\angle{P_2PP_3}+\angle{P_3PP_4}+\angle{P_4PP_5}+\angle{P_5PP_6}+\angle{P_6PP_7}\leqslant 180^{\circ}.$$所以 $\angle{P_1PP_2}$，$\angle{P_2PP_3}$，$\angle{P_3PP_4}$，$\angle{P_4PP_5}$，$\angle{P_5PP_6}$，$\angle{P_6PP_7}$ 这 $6$ 个分角中至少有一个不大于 $30^{\circ}$，不妨设 $\angle{P_1PP_2}\leqslant 30^{\circ}$．设 $PP_1=x$，$PP_2=y$，则\[\begin{split}P_1P_2^2&=x^2+y^2-2xy\cos {\angle{P_1PP_2}}\\&\leqslant x^2+y^2-2xy\cos{30^{\circ}}\\&=x^2+y^2-\sqrt 3 xy.\end{split}\]根据对称性，不妨设 $x\geqslant y$，由于$$\sqrt 3\leqslant y\leqslant x<3,$$所以$$P_1P_2^2=f(x)=x^2+y^2-\sqrt 3 xy=\left(x-\dfrac{\sqrt 3}{2}y\right)^2+\dfrac 14 y^2$$在区间 $[y,3)$ 上为增函数，因此\[\begin{split}P_1P_2^2&=f(x)<f(3)\\&=9+y^2-3\sqrt 3 y\\&=\left(y-\dfrac{3\sqrt 3}{2}\right)^2+\dfrac 94\\& \leqslant \left(\sqrt 3-\dfrac{3\sqrt 3}{2}\right)^2+\dfrac 34\\&=3,\end{split}\]而 $P_1P_2<\sqrt 3$ 与条件矛盾，因此假设不成立，所以引理得证．
下面利用引理证明本题结论．
根据引理，从 $P_1$ 出发的 $34$ 条线段 $P_1P_2$，$P_1P_3$，$P_1P_4$，$\cdots $，$P_1P_{35}$ 中至多有 $6$ 条线段的长度小于 $3$，即至少有 $28$ 条线段的长度不小于 $3$，不妨设线段 $P_1P_2,P_1P_3,P_1P_4,\cdots P_1P_{29}$ 的长度不小于 $3$．
再考察从 $P_2$ 出发的 $27$ 条线段 $P_2P_3,P_2P_4,P_2P_5,\cdots ,P_2P_{23}$，根据引理，这 $27$ 条线段中至多有 $6$ 条线段的长度小于 $3$，即至少有 $21$ 条线段的长度不小于 $3$，不妨设线段 $P_2P_3,P_2P_4,P_2P_5,\cdots ,P_2P_{24}$ 的长度不小于 $3$．
再考察从 $P_3$ 出发的 $20$ 条线段 $P_3P_4,P_3P_5,P_3P_6\cdots ,P_3P_{23}$，根据引理，这 $20$ 条线段中至多有 $6$ 条线段的长度小于 $3$，即至少有 $14$ 条线段的长度不小于 $3$，不妨设线段 $P_3P_4,P_3P_5,P_3P_6,\cdots ,P_3P_{17}$ 的长度不小于 $3$．
再考察从 $P_4$ 出发的 $13$ 条线段 $P_4P_5,P_4P_6,P_4P_7,\cdots ,P_4P_{17}$，根据引理，这 $13$ 条线段中至多有 $6$ 条线段的长度小于 $3$，至少有 $7$ 条线段的长度不小于 $3$，不妨设线段 $P_4P_5,P_4P_6,P_4P_7,\cdots ,P_4P_{11}$ 的长度不小于 $3$．
这样得到 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$，根据前面的讨论，这 $5$ 个点中任意两点之间的距离不小于 $3$．
所以，结论成立．
答案
解析
备注
