如图，$\triangle{ABC}$ 的内心为 $I$，$M,N$ 分别是 $AB,AC$ 的中点，$AB>AC$，内切圆 $\odot I$ 分别与边 $BC,CA$ 相切于 $D,E$；证明：$MN,BI,DE$ 三线共点．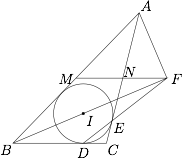
【难度】
【出处】
2011年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
如图，设 $MN,BI$ 交于点 $F$，连 $AF,AI,IE,EF$．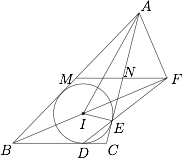
由于中位线 $MN\parallel BC$，以及 $BF$ 平分 $\angle B$，则$$MF=MB=MA,$$所以$$\angle{AFB}=90^{\circ},$$因 $IE\perp AE$，得 $AFEI$ 共圆，从而$$\begin{split}\angle{AEF}&=\angle{AIF}=\angle{IAB}+\angle{IBA}\\ &=\dfrac A2+\dfrac B2\\ &=90^{\circ}-\dfrac C2.\end{split}$$连 $DE$，在 $\triangle{CDE}$ 中，由于切线 $CD=CE$，所以$$\begin{split}\angle{CED}&=\angle{CDE}=\dfrac 12(180^{\circ}-C)\\ &=90^{\circ}-\dfrac C2\\ &=\angle{AEF},\end{split}$$因此 $D,E,F$ 三点共线，即有 $MN,BI,DE$ 三线共点．
由于中位线 $MN\parallel BC$，以及 $BF$ 平分 $\angle B$，则$$MF=MB=MA,$$所以$$\angle{AFB}=90^{\circ},$$因 $IE\perp AE$，得 $AFEI$ 共圆，从而$$\begin{split}\angle{AEF}&=\angle{AIF}=\angle{IAB}+\angle{IBA}\\ &=\dfrac A2+\dfrac B2\\ &=90^{\circ}-\dfrac C2.\end{split}$$连 $DE$，在 $\triangle{CDE}$ 中，由于切线 $CD=CE$，所以$$\begin{split}\angle{CED}&=\angle{CDE}=\dfrac 12(180^{\circ}-C)\\ &=90^{\circ}-\dfrac C2\\ &=\angle{AEF},\end{split}$$因此 $D,E,F$ 三点共线，即有 $MN,BI,DE$ 三线共点．
答案
解析
备注
