如图,抛物线 $ y=-x^2-6x-5 $ 与 $x $ 轴交于点 $A\left(-5,0\right) $,$B\left(-1,0\right) $,与 $y $ 轴交于点 $C\left(0,-5\right) $,点 $P $ 是抛物线上的动点,连接 $PA$,$ PC $,$PC$ 与 $x $ 轴交于点 $D $.过点 $P $ 作 $y $ 轴的平行线交 $ x$ 轴于点 $H $,交直线 $AC $ 于点 $E $,$\triangle APE$ 能否为等腰三角形?若能,请求出此时点 $P $ 的坐标;若不能,请说明理由.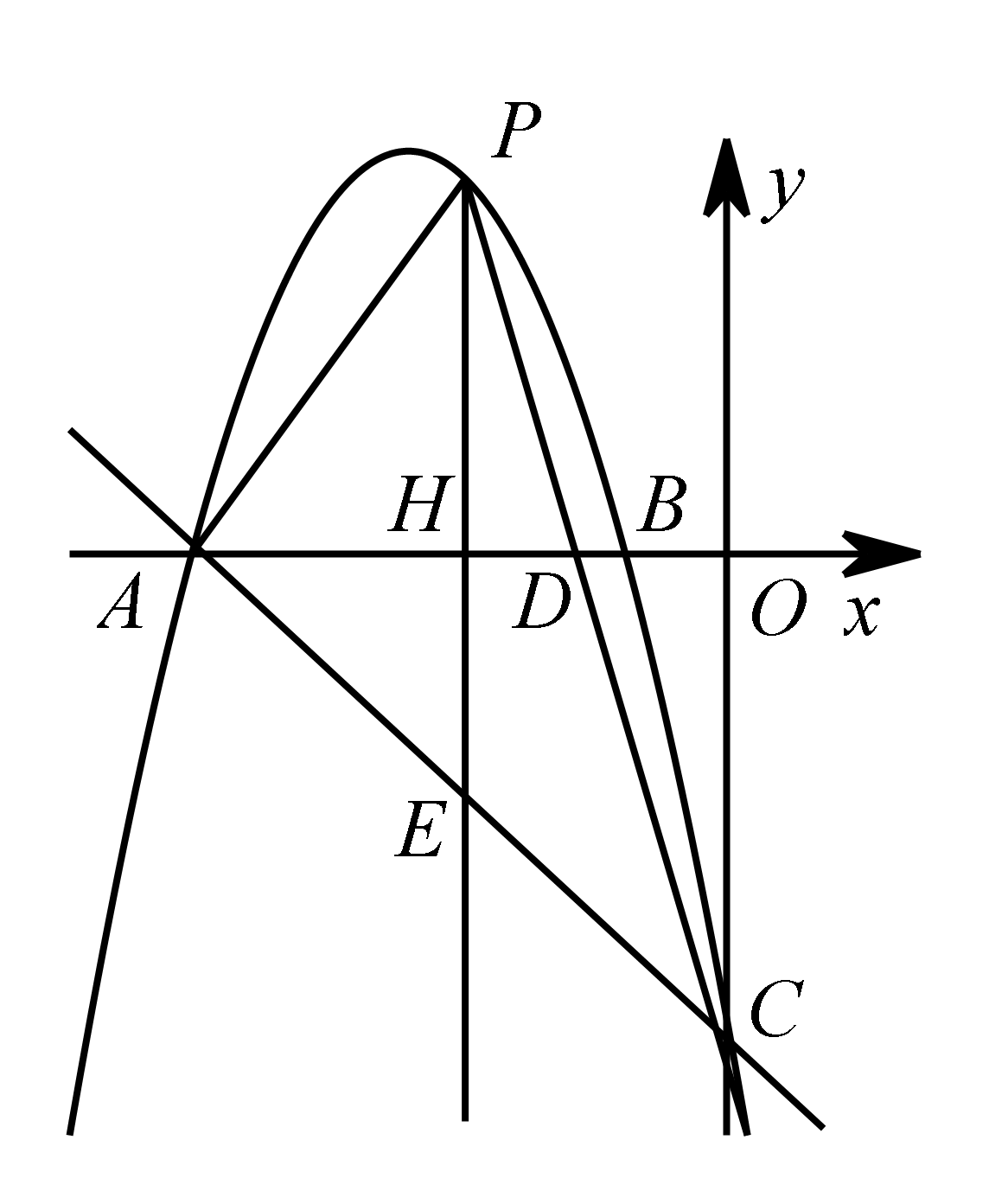

【难度】
【出处】
无
【标注】
【答案】
① 当 $ E$ 在线段 $ AC $ 上时.
i)当 $ PA=PE $ 时.
由 $ OA=OC=5 $,得 $ \angle AEP=\angle PAE=\angle ACO=45^{\circ} $,
$\therefore$ $ \angle APE=90^{\circ} $.此时点 $ P $ 与点 $ B $ 重合.
$\therefore$ 此时点 $ P $ 的坐标为 $ \left(-1,0\right) $.
ii)当 $ AP=AE $ 时.由题意得 $ \angle APE=\angle AEP=45^{\circ} $.
又 $ PH\perp AO $,
$\therefore$ $ AH=PH $,即 $ -x^2-6x-5=x+5 $.
解得 $ x_1=-2 $,$ x_2=-5 $(舍).
$\therefore$ 点 $ P $ 的坐标为 $ \left(-2,3\right) $.
② 当 $ E $ 在线段 $ AC $ 延长线上时.
$\because$ 点 $ A $,$ C $ 的坐标分别为 $ \left(-5,0\right) $,$\left(0,-5\right) $,
$\therefore$ 直线 $ AC $ 的解析式为 $ y=-x-5 $.
$\therefore$ 点 $ E $ 的坐标为 $ \left(x,-x-5\right) $.
i)当 $ PA=PE $ 时.
$ PE=-x-5-\left(-x^2-6x-5\right)= x^2+5x $.
又 $ AE=\sqrt{2}AH=\sqrt{2}\left(x+5\right) $,
则 $ x^2+5x=\sqrt{2}\left(x+5\right) $.
$\therefore$ $ \left(x+5\right)\left(\sqrt{2}-x\right)=0 $.
解得 $ x_1=\sqrt{2} $,$ x_1=-5 $(舍).
ii)当 $ x=\sqrt{2} $ 时,$ y=-6\sqrt{2}-7 $.
$\therefore$ 此时点 $ P $ 的坐标为 $ \left(\sqrt{2},-6\sqrt{2}-7\right) $.
线段 $ CA $ 的延长线上不存在点 $ E $,使 $\triangle APE$ 为等腰三角形
综上所述可得点 $ P $ 的坐标为:$ \left(-2,3\right) $,$ \left(-1,0\right) $,或 $ \left(\sqrt{2},-6\sqrt{2}-7\right) $
i)当 $ PA=PE $ 时.
由 $ OA=OC=5 $,得 $ \angle AEP=\angle PAE=\angle ACO=45^{\circ} $,
$\therefore$ $ \angle APE=90^{\circ} $.此时点 $ P $ 与点 $ B $ 重合.
$\therefore$ 此时点 $ P $ 的坐标为 $ \left(-1,0\right) $.
ii)当 $ AP=AE $ 时.由题意得 $ \angle APE=\angle AEP=45^{\circ} $.
又 $ PH\perp AO $,
$\therefore$ $ AH=PH $,即 $ -x^2-6x-5=x+5 $.
解得 $ x_1=-2 $,$ x_2=-5 $(舍).
$\therefore$ 点 $ P $ 的坐标为 $ \left(-2,3\right) $.
② 当 $ E $ 在线段 $ AC $ 延长线上时.
$\because$ 点 $ A $,$ C $ 的坐标分别为 $ \left(-5,0\right) $,$\left(0,-5\right) $,
$\therefore$ 直线 $ AC $ 的解析式为 $ y=-x-5 $.
$\therefore$ 点 $ E $ 的坐标为 $ \left(x,-x-5\right) $.
i)当 $ PA=PE $ 时.
$ PE=-x-5-\left(-x^2-6x-5\right)= x^2+5x $.
又 $ AE=\sqrt{2}AH=\sqrt{2}\left(x+5\right) $,
则 $ x^2+5x=\sqrt{2}\left(x+5\right) $.
$\therefore$ $ \left(x+5\right)\left(\sqrt{2}-x\right)=0 $.
解得 $ x_1=\sqrt{2} $,$ x_1=-5 $(舍).
ii)当 $ x=\sqrt{2} $ 时,$ y=-6\sqrt{2}-7 $.
$\therefore$ 此时点 $ P $ 的坐标为 $ \left(\sqrt{2},-6\sqrt{2}-7\right) $.
线段 $ CA $ 的延长线上不存在点 $ E $,使 $\triangle APE$ 为等腰三角形
综上所述可得点 $ P $ 的坐标为:$ \left(-2,3\right) $,$ \left(-1,0\right) $,或 $ \left(\sqrt{2},-6\sqrt{2}-7\right) $
【解析】
略
答案
解析
备注