如图,在圆内接四边形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 交于点 $E$,且 $\angle{ABD}=60^{\circ}$,$AE=AD$.延长 $AB,DC$ 交于点 $F$,求证:点 $B$ 为 $\triangle{CEF}$ 的外心.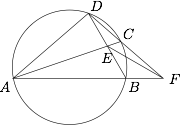

【难度】
【出处】
2011年全国高中数学联赛陕西省预赛二试
【标注】
【答案】
略
【解析】
因为 $AE=AD$,$A,B,C,D$ 四点共圆,所以$$\angle{BCE}=\angle{ADE}=\angle{AED},$$故 $BC=BE$.
又因为\[\begin{split}&{\begin{split}\angle{BCF}&=\angle{BAD}=180^{\circ}-(\angle{ABD}+\angle{ADB})\\&=120^{\circ}-\angle{ADE},\end{split}}\\&{\begin{split}\angle{BFC}&=\angle{ABD}-\angle{BDF}\\&=60^{\circ}-\angle{BAC}\\&=60^{\circ}-(\angle{AED}-\angle{ABE})\\&=120^{\circ}-\angle{AED}.\end{split}}\end{split}\]且$$\angle{ADE}=\angle{AED},$$所以 $\angle{BCF}=\angle{BFC}$,则 $BC=BF$.
因此$$BC=BE=BF,$$故点 $B$ 为 $\triangle{CEF}$ 的外心.
又因为\[\begin{split}&{\begin{split}\angle{BCF}&=\angle{BAD}=180^{\circ}-(\angle{ABD}+\angle{ADB})\\&=120^{\circ}-\angle{ADE},\end{split}}\\&{\begin{split}\angle{BFC}&=\angle{ABD}-\angle{BDF}\\&=60^{\circ}-\angle{BAC}\\&=60^{\circ}-(\angle{AED}-\angle{ABE})\\&=120^{\circ}-\angle{AED}.\end{split}}\end{split}\]且$$\angle{ADE}=\angle{AED},$$所以 $\angle{BCF}=\angle{BFC}$,则 $BC=BF$.
因此$$BC=BE=BF,$$故点 $B$ 为 $\triangle{CEF}$ 的外心.
答案
解析
备注